Площта на фигурата, ограничена от линии

Инструкции. За решения влизат функцията в форма у = f1 (X); у = f2 (х).

Пример №1. Изчислява областта на фигурата, ограничена от линии и х + у = 6.
Решение. Ние построи координатна система XOY тези редове. Ние намираме в точката на пресичане на тези редове

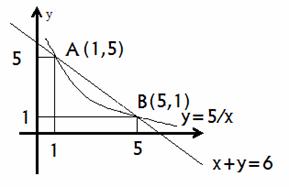
Фиг.1. Квадратна форма.

Ние означаваме тези точки от А и В. По този начин, (1, 5), В (5: 1). Зоната за търсене S е равна на разликата от квадратите на фигурата ограничени от линиите, х = 1, х = 5, у = 0, у = 6-х (означен областта чрез S1) и линиите х = 1, х = 5, у = 0, (този площ означен S2). по този начин
S = S1 - S2
S2 Районът може да се изчисли с помощта на определен интеграл
2 единици.
S1, може да бъде изчислена като сума от квадратите на правоъгълен триъгълник и правоъгълник, но все пак удобно да се изчисли неразделна S1
.
Сега можете да се изчисли необходимата площ
S = S1 - S2 = 12-5 lN5
Отговор: S = 12 - 5 lN5 единици 2.