Площта на фигурата, ограничена от линии - Форум - Казахстан и образование - образователно уебсайт

Сега нека да се научите как да се намери областта на фигурата, образувана от два реда.

Определя се площта на фигурата, ограничена от линиите у = х + 3, у = 2-х и оста на абсцисата.

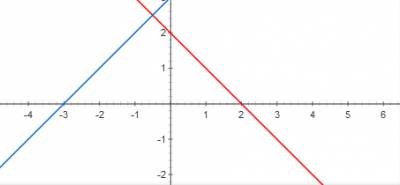
1 начин да се реши просто, намиране на пресечна точка на графиката:

У координата на модула е с височина триъгълник.

Ние намираме пресечната точка на правите линии с говедото на ос, вместо да замени у 0 във всяка уравнение:

дължина на основата е сумата от х координата на пресичане с равнина ОХ взети по модул:

Според формулата, знаейки, височината на основата на триъгълника и се намери лицето й:

2 Метод, установяването на основните теорема формула:

Формулата е следната:

В него е записано като неразделна от А до точка Б, а

За решаване на определен интеграл, ние първо трябва да се намери примитивна функция F (X) за F на функция (х). И след това се намери разликата между стойностите на А и Б в заместения примитивен F (х) на.

Сега обратно към нашия пример, първо обърнете внимание, че нашата област на региона е възможно да се изчисли сумата на две определени интеграли: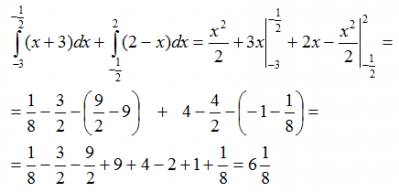

Както можете да видите първия метод е по-лесно да се реши, обаче, не винаги е възможно да го използвате, защото освен от правия и могат да бъдат извити линии. Нека ги разгледаме в следния пример.

? 200 '200px': '' + (this.scrollHeight + 5) + 'пиксела ");"> изчислява площта на фигурата, ограничена от линиите у = х ^ 2-2x + 2, у = х, у = 2x-1

Преди да започнете да направи определен интеграл видите кои линии са на графиката:

у = Х-2х + 2 - парабола на формуляра Y = ax² + BX + C, клон насочена нагоре, на върха е в точка с координира х = Ь / 2а, х = 2/2 = 1, у = 1. А (1,1)

у = х и у = 2x-1, се пресичат в точка А (1,1)

(В изображението желаната област е избрана, точката на пресичане е посочено Разписание)

За дадена област на необходимото пространство фигура 1, фигура 2 поемане област и областта на фигура 3, фигура 3 се получава от разликата в област между площта 4 и фигура 5.

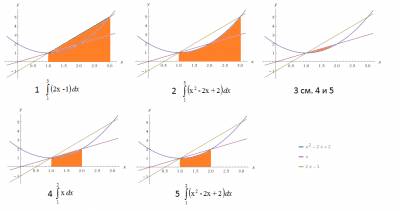
Данните показват определени интеграли за изчисляване, за всеки примитивен находка и замени първото горната точка след това ги изважда от дъното.

3) (3/2) - (4/3) = (9-8) / 6 = 1/6

Квадратни форми, избрани в първата снимка е:

10 - (14/3) - (1/6) = (60-28-1) / 6 = 31/6

? 200 "200px ':' '+ (this.scrollHeight + 5) +' пиксела"); "> Y = 1/3 ^ 3, у = 3

За решаването на тези проблеми, това е много важно, за да могат да изследват функцията и изграждане на графици бързо, най-малко схематично.

Ние започва с първата функция у = (1/3) * х 3

Като каза, трета степен, че е графика на кубичната парабола и е спираловидна крива, преминаваща през началото на първия до третото тримесечие.

По този начин, както в х = 0, у = 0 графика преминава през центъра координира.

Цифрата е, както следва:

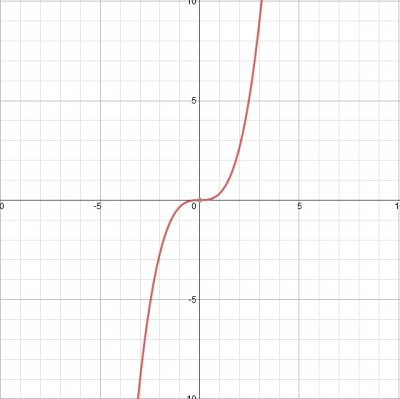
Сега втората функция у = 3, също преминава през произхода и права линия.

Сравнителен графика две функции да видите желаната област:

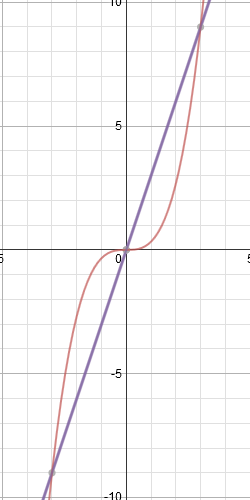
Както можем да видим, за да получите две симетрични фигури, една от първите, и един през третото тримесечие.

За да намерите общата площ е достатъчна, за да се намери някой от тях и се умножава по две.

Намираме пресечната точка на графиките на функции, достатъчно е да се равнява двете функции (1/3) * х 3 = 3x:

1 точка (0, 0), точка 2 (3, 9)

Площта на фигурата, ограничена от кривите Y = f1 (х) и у = f2 (х) [f1 (х) ≤ f2 (х)] и директно х = А, X = б се изчислява с помощта на формулата у = f1 (х) и у = f2 (х) [f1 (х) ≤ f2 (х)] и директно х = а, X = б се изчислява по формулата

В нашия случай, е под формата:

Остава да се намери примитивен:

След това нанесете формулата на Нютон-Лайбниц за определен интеграл:

S = F (б) - F (а) = F (3) - F (0)

След областта от 0 до 3 в графиката е равна 27/4

Пълният областта на фигурата, ограничена от линиите е 27/2