ОБЛАСТ допустимите стойности

Сайт Математик Фелдман Инна Владимировна. Професионални услуги преподавател по математика в Москва. Подготовка за ДПА и изпита, да помогне на изоставащите.

Диапазонът на допустимите стойности на алгебрични изрази (съкратено ТСС) - набор от стойности на променлива, в която се определя този израз.

В хода на учебната алгебра има пет основни функции. които имат ограничен домейн. Ето кои са те:

Изразяване под знака на корен дори кратност, трябва да бъде по-голяма или равна на нула.

Изразът в знаменателя не може да бъде нула.

Изразяване под знака на логаритъм трябва да е строго по-голямо от нула; изразяването на основата на логаритъма трябва да е строго по-голямо от нула и се различава от единство.

5.Est две функции, които съдържат "скрит" фракция:

Степента на корен - естествено число, различни от 1.

По този начин, функциите и имат друг домейн.

Ако изразът съдържа една или повече функции, които са определени за ограничен набор от стойности на аргумента, за да намерите изразът DHS, е необходимо да се вземат предвид всички ограничения, наложени от тези функции.

За да намерите широка гама от допустимите стойности на изрази, че е необходимо да се провери дали по отношение на функция са налице, което имам изброени по-горе. А що се отнася до откриването на тези функции, ограничения за записване поискали от тях, движейки се от "извън", "вътре".

Нека обясня с пример:

Намерете областта на функцията:

За да намерите областта на функцията. да открие границите на допустимите стойности на изрази. който се намира от дясната страна на функциите на уравнението

Аз специално избра "ужасен", на пръв поглед, да функционира, за да ви покажа какво проста операция е разбит намиране на процеса на толеранс.

"Crawl" изражението на дясната ръка:

1. Ние виждаме един изстрел:

В знаменателя не е нула. напишете:

2. Ние виждаме в знаменателя на логаритъм:

Изразяване под знака на логаритъм трябва да е строго по-голямо от нула; изразяването на основата на логаритъма трябва да е строго по-голямо от нула и се различава от единство.

3. Намираме корен квадратен:

Изразяване под знака на корен дори кратност, трябва да бъде по-голяма или равна на нула.

Сега запишете всички ограничения в системата на неравенството:

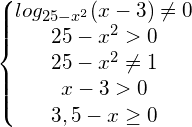
Решението на тази система на неравенството погледнете VIDEUROKE: