Как да се увеличи броя на простите числа 2

Запис на номера на хартиен носител (по-горе). Според редица изготви две диагонални линии - едната насочена към правото, а втората - от ляво. Или напишете номера по-долу, и да изготви две диагонални линии над него. Пример: Поставете по-председател множители на 315. 315. /. \

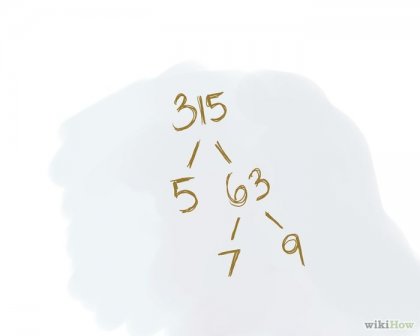
За всеки от двата множители го напиша няколко фактора. Чифт множители - две числа, чиито продукт е равен на оригиналния номер. Не пишете мултипликатори за прости числа. Пример. 315 /. \. 5. 63 / \. 7. 9

Търсене за всяка двойка на факторите на определен брой. Чифт множители -. Две числа, чийто продукт е равна на първоначалния брой [1] Тези два фактора трябва да бъдат написани под наклонените линии. Можете да изберете всеки два фактора. Крайният резултат не зависи от вашия избор. Имайте предвид, че ако този брой двойки множители не (с изключение на 1 и на самата броя), тя е просто число, и то не може да бъде фактор. Пример. 315 /. \. 5. 63

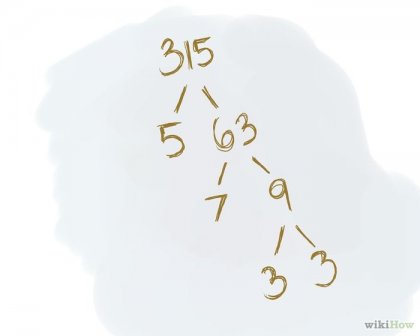
Повторете процеса, докато не остане само прости числа (прости числа). Председател номер - число, което се дели само по себе си и 1. Продължете да изготви диагонални линии и запис чифт множители толкова дълго, колкото и борбата с прости числа. Моля, обърнете внимание, че вашата дървовидна структура, броят на множители 1 не трябва да бъде. Пример. 315 /. \. 5. 63. / .. \. 7. 9. / .. \. 3. 3

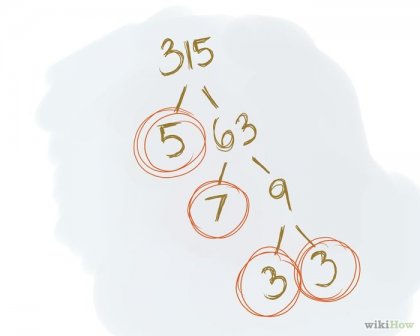
Веднага след като се сблъскват с просто число (председател на множители), изберете го (кръг или подчертан), за да се избегне загубата на многоразклонената структура фактори. Пример: основните фактори са номера 5, 7, 3, 315. 3. /. \. 5. 63. / .. \. 7. 9. / .. \. 3. 3 Алтернатива: прехвърляне на основните фактори за всяко следващо ниво на дървовидната структура и фактори, така че да не ги загубите - всички прости фактори ще се намира на най-ниското ниво [2]. Пример. 315 /. \. 5. 63. /. / .. \. 5. 7. 9. /. /. / .. \ 5. 7. 3. 3

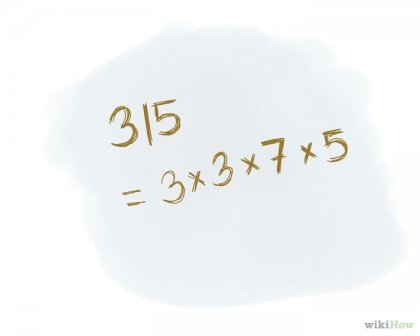
Отговорът е написан като продукт на основните фактори. [3] Ако учителят е длъжен да напише отговора под формата на дървовидна структура на множители, оставете нещата такива каквито са; в противен случай се записва отговор, както следва: Пример: 5 * 7 * 3 * 3

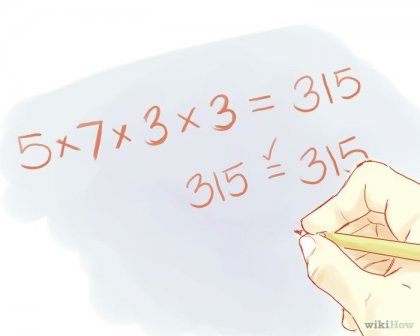
Проверете отговора. Умножете получените основните фактори, и вие трябва да получите оригиналния номер. Пример: 5 * 7 * 3 * 3 = 315

След разпадането на номера на прости числа запишете всички председатели фактори за всеки номер. След това изберете или напишете всички общи фактори (факторите, които са присъщи на всеки списък на основните фактори). Ако списъците няма общи фактори, тогава GCD = 1. Пример: общи основните фактори номера 195 и 260 са числата 5 и 13.

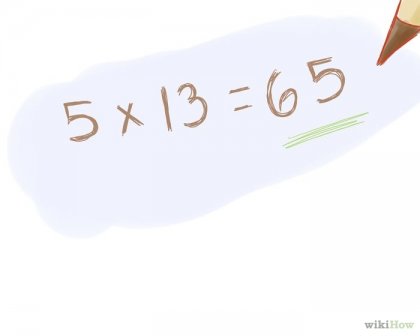
Размножава общи фактори. [4] Ако тези цифри са няколко често срещани основните фактори, е необходимо да ги умножи да намерите НОД. Ако тези цифри само един общ основен фактор, тя е равна на НОД. Пример: общи фактори номера 195 и 260 са 5 и 13. тях се размножава и да: 5 * 13 = 65

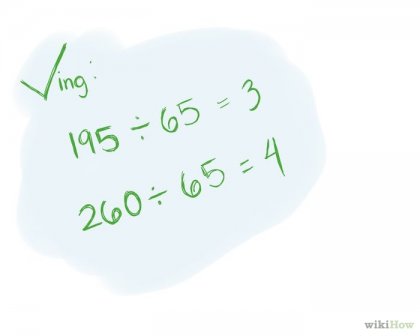
Напишете отговора. Двойна проверка на данните за отговор като се раздели броят сте намерили на НОД. Ако цифрите падат GBR равномерно, тогава отговорът е правилен. Пример: GCD номера 195 и 260 е равно на 65. 195/65 = 3. 260/65 = 4.

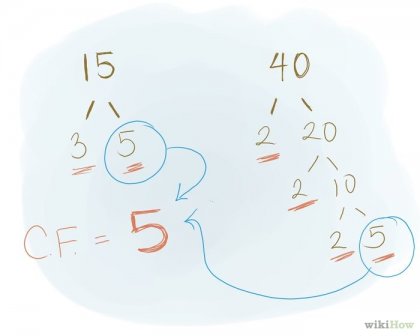
След разпадането на номера на прости числа запишете всички председатели фактори за всеки номер. След това изберете или напишете всички общи фактори. Моля, имайте предвид, че ако са дадени три (или повече) на броя на общи фактори, трябва да присъстват в списъка на фактори най-малко две цифри на данни (а не всеки фактор в списъка). Да не се включва двойна множители. Например, ако в списъка на фактори първите на множителя 2 присъства два пъти, а в списъка на фактори втори на множителя 2 има само един път, ще трябва да се отбележи един 2 в първия списък, както и 2 във втория (т.е. втората 2 в първия списък, не счете ). Пример: общи фактори номера 15 и 40 е само номер 5.

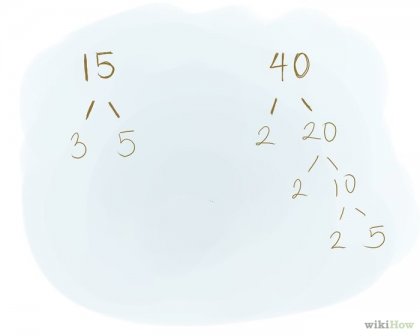
За да намерите най-малкото общо кратно (НОК) на две или повече числа трябва да се разложи тези номера в основните фактори. За тази цел се използва метода, описан по-горе. Вие ще трябва да се създаде структура дърво за всеки един от факторите. За тази цел се използва метода, описан по-горе. NOC - е най-малкият брой, който се дели на всеки един брой. Пример: Намерете най-малкото общо кратно на 15 и 40. 15. / .. \. 3. 5 основните фактори на броя 15 са 3, 5. 40. /. \. 5. 8. / .. \. 2. 4. / \. 2. 2-председатели фактори на 40 са числата 5, 2, 2, 2.

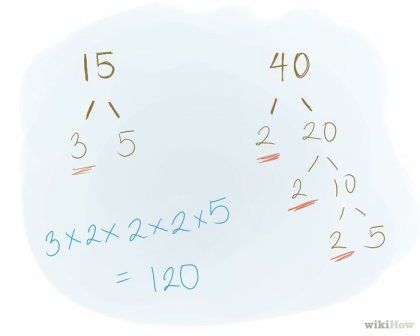
Умножете общите фактори и всички фактори, които не са широко разпространени. Така се взема предвид всички фактори, които не са широко разпространени. В горния пример, вторият 2 в първия списък трябва да бъдат взети под внимание. Общият коефициент се третира като единен номер. Пример: Общият фактор е броят 5. множители, които не са споделени, броят ще бъде 3, 2, 2, 2. По този начин, е необходимо да се размножават: 5 * 3 * 2 * 2 * 2 = 120.

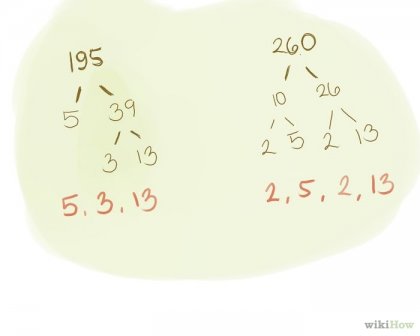
За намиране на най-голям общ делител (ГРУ) на две или повече числа, което трябва да се разлага тези номера в основните фактори. За тази цел се използва метода, описан по-горе. Вие ще трябва да се създаде структура дърво за всеки един от факторите. За тази цел се използва метода, описан по-горе. NOD - е най-големият номер, който равномерно разпределя всеки даден номер. Пример: намерите НОД на числата 195 и 260. 195. /. \. 5. 39. /. \. 3. 13 основните фактори на 195 са числата 3, 5, 260. 13. /. \. 10. 26. /. \ ... / .. \ 0.2. 5. 2. 13-председатели фактори на 260 са числа: 2, 2, 5, 13.

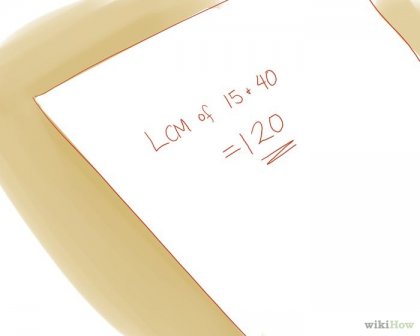
Напишете отговора. Пример номера НОК 15 и 40 ран 120.

256338 256339 256340 256341 256342 256343 256344 256345 256346 256347 256348 256349 256350 256351