Числен серия, математика, онлайн решение!
Гръцки математика до голяма степен са доминирани от геометрията и много време, прекарано отчитане на броя на точките, разположени в една равнина, под формата на различни геометрични фигури. Броят на точките, които представляват
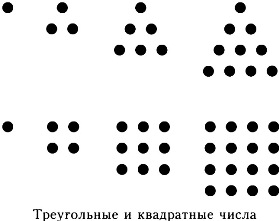
Можем да си представим sverhmikroskopichesky триъгълник, състоящ се от една точка. Три точки също образуват триъгълник, в който две точки от всяка страна. Шест точки са вече по-голям триъгълник, чиито три точки от всяка страна, както и на десет точки - триъгълник, чиито четири точки от всяка страна.
Може ли да бъде написана в няколко триъгълни числа: 1, 3, 6, 10, 15, 21. 28, 36, 45, 55, и така нататък. Всеки следващ брой триъгълни форми триъгълник, в които от всяка страна в една точка повече. Редица триъгълни числа е безкраен.
Моля, имайте предвид, редица триъгълни числа образува определена зависимост. Първият брой е равен на 1, по-долу е 3, т.е., 1 + 2, последвано от 6, т.е., 1 + 2 + 3, след това 10, т.е. 1 + 2 + 3 + 4, след това 15, т.е., 1 + 2 + 3 + 4 + 5, и така нататък. Запаметяването тази връзка, вие ще бъдете в състояние да продължи серията от триъгълни числа за неопределено време без да се правят триъгълници и брои точки. Определете дали даден броят на триъгълна или не е възможно, то представя под формата на серия, подобно на по-горе. Ако номерът може да се представи като сума от числа, в която всяко следващо число е едно повече от предишния, и първото число е самоличността, а след това този номер - триъгълни.
Всяка група от числа, която може да бъде представена като поредица подчинявайки се на някои правило представлява поредица от цифри.
Цифрите са броя на точките, от които можете да направите квадрат, също могат да бъдат представени като поредица. Както миналия път, една точка може да се разглежда като sverhmikroskopichesky двойка
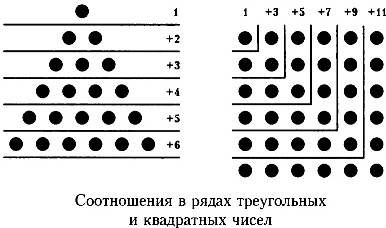
rehugolnik. Четири точки също образуват четириъгълник. където в две точки от всяка страна. Девет точки форма има по-голям правоъгълник, при което в три точки от всяка страна, а шестнадесет точки - четириъгълник чиито четири точки от всяка страна.
Може ли да бъде написана в редица четириъгълна: 1, 9, 16, 25, 36, 49 и така нататък. Всеки следващ брой четириъгълна образува които четириъгълник от всяка страна в една точка повече. Редица правоъгълни числа е безкраен.
След анализ на цифрите, които съставляват серия от четворни номера, виждаме, че те също са обект на определена връзка. Нека започнем с 1. Няма никакви опции, устройството - това е само един. Но 4 + 1 = 3, тогава 9 = 1 + 3 + 5, 16 = 1 + 3 + 5 + 7 и така нататък.
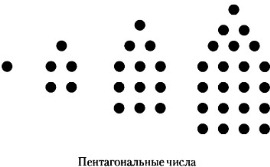
Съотношението между броя на триъгълни и квадратни фута редове показано на диаграмата.
Гърците са имали редица петоъгълни номера. които са представени на фигурата. Тази серия може да се разглежда като синтез на триъгълна и четириъгълна серия. Ако построим няколко петоъгълници по същия начин, както и вградените триъгълници и правоъгълници, получаваме серия от номера на формата 1, 5, 12, 22, 35, 51, 70 и така нататък. Това е поредица от числа, които се получават чрез добавяне на номера се различават един от друг от три. Първият план на поредицата - единица. II - 5, т.е. 1+ (1 + 3) = 1 + 4. Трето - 12, който е 1 + 4 + (4 + 3) = 1 + 4 + 7, четвъртата - 22, който е 1 + 4 + 7 + 10 и така нататък.
Гърците са измислили и други геометрични фигури. моделиране сериен номер. Числата, които правят тези последователности, наречени къдрава. Някои помислих, броят на симулирана плосък вече не е фигурира като един триъгълник и квадрат, и обемът, като кубове. Тези кубчета са трудни за изобразяване на снимката, но ако се вгледате в брой линия, можете да се направи някаква представа за кубичен формата на точките. Серия кубически номера - редица 1, 8, 27, 64, 125 и така нататък.
Няколко кубични числа също представя серия от суми нечетните числа. Въпреки това, тези суми не започват с един. Първият план на поредицата - 1 секунда - 8 + 5 или 3; третата - е 27 или 7 + 9 + 11; Четвърто - е 64 или 13 + 15 + 17 + 19. Всяка група от номера, които трябва да обобщим, започва с нечетен брой, следващ този, който завършва предишната сума, а броят на условия във всяка една от следните суми за един повече от предишната.
Сподели с приятели: