WolframAlpha на руски как да намерите областта на фигурата, ограничена от кривите

В една от предишните си постове, свързани с употребата на интегралното смятане, вече обсъжда как да се намери равна площ на фигурата в Wolfram | Alpha.

И това е казано, че зоната за заявка между тях. което от Wolfram | Alpha се използва за изчисляване на площта на равнинни фигури, използвайки интеграли работи правилно само в някои относително прости случаи. При по-сложни задачи, могат да се обръщат за "ръчно" метод - поетапно процедурата за изчисляване на площта на самолета фигура с помощта на интеграла. Това означава, че в първия етап на определяне на границите на интеграция, а след това с помощта на открити граници, изчисляване на определен интеграл - района на фигура. Как да го направя на практика, е описано в поста по-горе.

Въпреки това, за повечето приложения, особено за непушачи математици, това "ръчно" режим не е много удобно. Ето защо, Wolfram | Alpha предлага и други начини за това как да се намери областта на фигурата, ограничена от две криви.

На първо място, в най-простите случаи. Както вече бе споменато, площта между кривите може да бъде изчислена като се използва областта на заявката между:

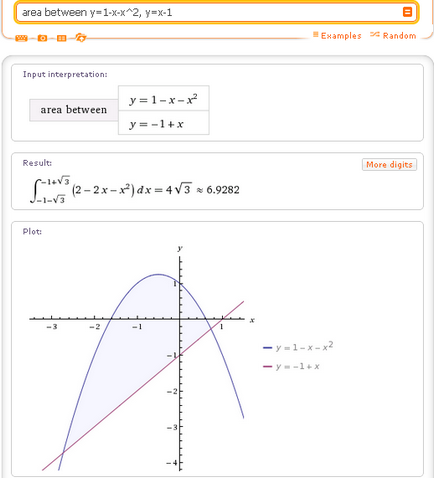
На второ място, ако знаете, че границите на интеграция. след това да се изчисли площта на фигурата, ограничена от две линии в района между заявката, можете да зададете допълнителен домейн (домейн) - сегмента на оста Ox, която се изчислява върху площ:

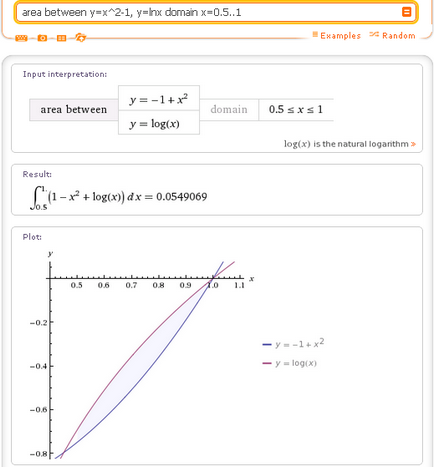
Ако сравните този резултат с този, който е бил преди това се получи при поискване интегрират lnx- (х ^ 2-1) DX, х = 0.450764..1. ще видите, че начина, по който район между. домейн. по-удобно, и отнема по-интуитивен резултат.

И накрая, ако искате да се изчисли зоната, ограничена от затворена крива. например, зоната вътре в елипсата, използвайте тази област заявка вътре:

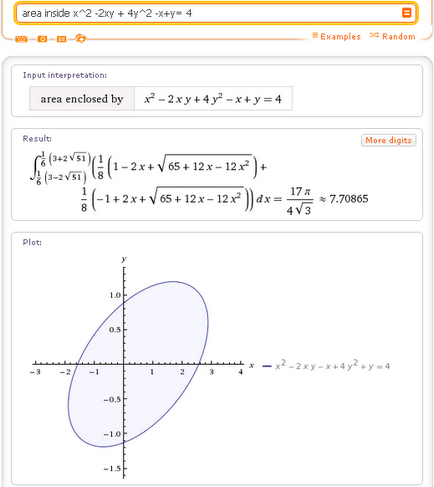
По този начин, за да се изчисли площта на самолета фигура, ограничена от криви линии, Wolfram | Alpha използва такива искания: област между тях. зона между тях. домейн. и района вътре.