В) се изчислява площта на фигурата, ограничена от
.
В) се изчислява площта на фигурата, ограничена от линии. , , ,
Решение. На първо място, извършване на чертежа:
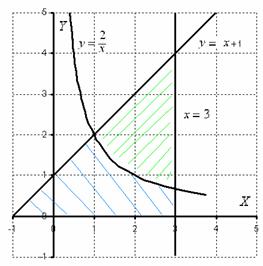
Цифрата, която е област, ние трябва да намерим сенчеста синьо (проверяват внимателно условието - какво цифра е ограничена). Но на практика, поради невнимание често е въпрос, на който трябва да се намери областта на фигурата, която се сенчести в зелено!
Този пример все още е полезен с това, че смята площта на фигурата с две определени интеграли. наистина:
1), разположени на сегмент над оста на линейната графика;
2) В сегмента над ос на графиката е хипербола.
Очевидно е, че зоната може (и трябва) да се добави на, така че:
Ние считаме, определени линии, пресичащи точка. За да направите това, ние се реши системата уравнения:
За да намерите абсцисата дадени линии на точки на пресичане решаване на уравнението:
По този начин, тази линия е парабола и правата линия се пресичат в точки А (-2, 0), В (4; 6).
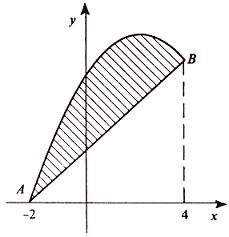
Тези линии образуват затворена форма, площта се изчислява по-горе формула:
Според намерите Нютон-Лайбниц:
а) Необходимо е да се намери определен интеграл
Така желания интеграл е равно на 6.
Пример 8. Намерете най-неопределени интеграли:
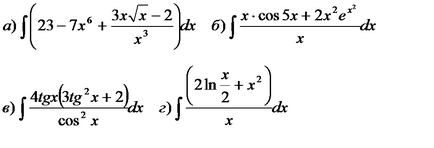
При решаването примери трябва да използват свойствата на неопределени интеграли, маса на интеграли, които включват формулата на неразделна линейна функция на аргумента, и директно включване на метода на смяна.
б) завършване termwise разделение в подинтегрален, получаваме:
г) Ние използваме заместване:
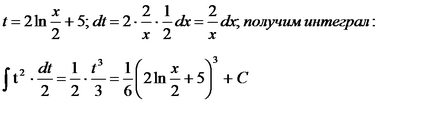
г) да се възползва от заместване:
1) Изчислява определени интеграли:
При изчисляването определени интеграли използване на основните теорема формула
. Получаване примитивна функция F (х) ще изпълнява или директно, или чрез заместване.

1) Извършване на операциите на събиране, изваждане, умножение, разделяне на комплексни числа в алгебрични форма.
За първи път се трансформира второто число, като се използват стойностите на степента на въображаемия уреда. и 18 = I 16 = I 2 + 2 и 16 2 = 1и = -1, т.е. 15 = I 12 + 3 12 = I 3 I 3 = и = -i, Z2 = -2 + 5i
Ние извършваме операции на номера:
а) съществува набор от многоцветни мъниста, сред които 5 синьо, червено и зелено 3 2. Ball произволно извлича 4. Намерете вероятността, че сред уроците мъниста 2 сини, 1 червена и 1 зелена.
За да се определи вероятността за случайна събитие ще използва класическата формула. където п - броят на всички възможни резултати, тили броя на резултатите благоприятен вид на събитието. Проблемът на тези ценности трябва да бъдат намерени с помощта на комбинации.
б) от картите раздели азбука, съставена думата "Панорама". Карти и произволно разбърква в продължение на една карта 5 се отстранява, като ги г. от порядъка на екстракция. Намерете вероятността, че ще бъде съставен от думата "роман".
В тази задача, можете да използвате продукта на независими случайни събития
И - да се захващаме на думата "романтика";
B1 - Екстракт от първата карта с буквата "р";
B2 - извличане на втората карта с буквата "о"; и т.н.
P (A) = Р (В1). Р (В2). Р (B3). Р (В4). Р (В5) =