Процедурата за решаване на проблемите на принципа на суперпозиция

Начало | За нас | обратна връзка

1.Prochitat задача; запишете всички зададени стойности на физични величини и да ги конвертирате в системата SI.

· На фигурата е изобразен разпределението на таксите, които произвеждат по-област;

· Изберете координатна система, като се вземат предвид симетрията на проблема;

· Определяне на всички разстояния, които са необходими за решаване на проблема, както и да се направи силата на вектори поле, генерирано от всяка такса разпределение до точката на интереси.

3. Напишете формулата за изчисляване на напрежението модули областта на индивидуалните такси за в даден момент.

4. За да проектират силните на всички вектори на оста на координатната, както и да намерят проекцията на общото интензивност вектора на всяка ос. Познаването на общия проекцията на вектора на координатните оси Ex. Ей и Ез. ние можем да се изчисли общата единица вектор с помощта на питагорова теорема.

Примери за решаване на проблеми при изчисляването на електрическите полета въз основа на принципа на суперпозиция

Намери електрическото поле в точките А и В
(Вж. Фиг.), Лежащ върху перпендикулярна ъглополовящата между такси точка q1 = 8 п и п q2 = -6, са във вакуум. Разстоянието между таксите R = 10 cm, AB = 4 см, д = 1.

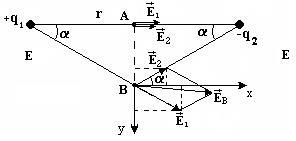
Фигурата показва разположението на таксите и точките А и В, за които ние трябва да намерим силата на полето, както и избора на координатната система е показано.

а) В точка А поле се създава от такси два точкови Q1 и Q2. По дефиниция, силата поле - е силата, с която устройството за зареждане поле за генериране работи на положителен заряд точка, разположена в точка А, така че векторът на напрежение в този момент в същата посока. Общият напрежение е сумата на напрегнатост на полето на отделните такси

или в проекция на OX оста

Пишем формулата за изчисляване на размера на полето интензитет на такси точкови Q1 и Q2 в точка А:

И ние стигнем до точката:

б). В точка В вектори и 2а са насочени под ъгъл един към друг и модулите на векторите не са еднакви, защото стойността на Q1 и Q2 различни такси.

Пишем формулата за изчисляване на размера на Q2 и точкови таксите за напрегнатостта на полето q1 в точка Б:

Всеки един от тези вектори дава проекция на двете оси:

Прогнозите общия интензитет вектор в точка В ще бъде равен на:

Сега е възможно да се получи формула на Питагоровата теорема за изчисляване на модула на вектора на електричното поле, генерирани в Q1 на такси точка Б и Q2. ,

С всички изрази, получени по този алгебрични преобразувания, ние се получи крайния израз за изчисляване на желаните количества:

Изчисляваме цифровата стойност от общото поле на точка Б:

Забележка. В някои случаи, когато решението се дължи на доста тромави алгебрични преобразувания, ние можем да се калкулира в хода на решаването на проблема. Така че това е възможно да се направи, и да се реши този проблем.

A: електрически напрегнатостта на полето в точка А е
ЕА = 50.4 кВ / m и е насочено от заряда на Q2 отговаря на Q1. В точка В, напрежението се равнява на U = 24.1 кВ / m и посоката е показано.

3. Пример 1. Две дълги нишка като заредени разположени R1 = 10 см един от друг. Плътността на линеен заряд са еднакви и равни на = 10mkKl / m.

Виж големината и посоката на получената напрегнатостта на полето в точката А, всяка нишка дистанционно от разстояние а = 10 cm.

Електростатични полета, генерирани от различни разпределения на такси се формират на принципа на суперпозиция във всяка точка в пространството. Като се има предвид симетрията на проблема, направи рисунка, поставянето на нишката, перпендикулярна на равнината на чертежа. Точка отстранява от двете вериги на разстояние а = r1 .Poluchili равностранен триъгълник. За да разберете посоката на интензитета на вектор поле, генерирано в точката такса всяко влакно пусната в този процес точка такса "1" и да решат как прежди полета действат на тази такса. Тъй като нишките са положително заредени, те ще отблъсне заряд тестове и вектора и ще бъдат насочени както е показано. Vector общия интензитет на поле, в съответствие с принципа на суперпозиция, намиращ се на правилото за успоредник.

Силата на взаимодействието на тези заредени нишки зависи от разстоянието между тях, така че работата на електростатичен напрегнатостта на полето трябва да се изчисляват чрез интегрална когато удължени нишки.

1) Може да се види, който сочи към правото, а модулът може да се намери на:

2) Силата на взаимодействието на заредени нишки зависи от разстоянието между тях. Всяка нишка създава поле, а това поле действа върху заряда на друга тема. - силата поле на първата спирала.

-силата на единица дължина на втората спирала е:

Работата на тази сила може да бъде изчислена като:

Да вземем на интеграл от функцията. Всички константи вземат от неразделна знака и да получат табличен интеграл, който е равен на натуралния логаритъм на аргумента.

Ние замени границите на интеграция и ние най-накрая получи:

Използвайки данните на проблема, ние се получи числен отговор

Положителния заряд на р = 5 х 10 -8 Kd равномерно разпределени тънка тел semiring радиус R = 20 см. За определяне на силата на полето Е в центъра на semiring.

р = 5 х 10 -8 Kd;

Анализ и решение. В тази задача, областта, произведен от Q на зареждане, разпределени през тънки полупръстените с радиус R. Плътността на линеен заряд е :. За такъв случай не можете директно да използвате формулата за интензивността на полето на такса за точка или заредена безкрайна спиралата. Такъв проблем може да бъде решен с помощта на принципа на суперпозиция. Разделете цялото ръководство за по много малки парцели дължина дл. при всеки отчетен заряд DQ = т х дл. Такава зареждане може да се разглежда като стойност точка и интензивността на полето на заряда изчислява по формулата

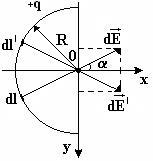
Фигурата показва избора на координатните оси и поле вектор. генерирани при О заряд .Given симетрия на проблема, който е еталонната точка координатна система, свързана с точка O, в центъра на половина пръстени и за предаване на координатните оси, както е показано.

Ние проектираме вектора на координатните оси:

Това се вижда от симетрия че всеки елементарен заряд DQ там е разположен симетрично спрямо оста OX заряд DQ ¢ на. Проекцията на напрегнатост на полето на тези такси по оста у ще даде нула при всички ъгли на един.

Така, че е необходимо да се намерят само общия проекцията на вектора на оста х. Разбираемо е, че в случай на непрекъснато разпределение на разходите трябва да бъде заменен от сумиране на интеграция по цялата дължина на кабела, на която плащането.

В подинтегрален включва две променливи л и. Като се има предвид, че и DL = Rd е, да замени променливата на интеграция и да получи

Фигурата показва, че. а.

A: напрегнатостта на полето в центъра на пръстена, е равна на 7,2 кВ / m.

Фигурата показва зареден безкрайна равнина с равнината на повърхността на заряда SCLC S = 40 / т2, и като заредена шийката с маса m = л г и зареждане р = 1 п. Какво ъгъл с равнината образува нишка, на която виси на топката?

Таксата е в равнината на терена. Той работи върху три топка сила, изобразено на фиг. Пишем състоянието на равновесие топка.

Ние проектираме полученото уравнение за координатните оси:

Решаването на системата от уравнения, получаваме Фел. = Mg х TGA. ,

От друга страна, Фел. = QE. където E - електрическо поле, създадено от една безкрайна равнина.

От получената система от уравнения имат

Невярно е безкрайна равнина може да се изрази по следния начин:

В този случай, заряда и равнината на въздуха, т.е. д = 1.

TGA = 0,2259 »0226

A: Нишката е равнинен ъгъл а от 13 = 0.