Примери за решаване на проблеми, свързани с "интензитет на електрическото поле

При решаването на проблеми с помощта на концепцията за електрически напрегнатостта на полето, трябва първо да знае формулата (14.8) и (14.9) определяне на силата, действаща по обвинение от електрическото поле, и интензивността на полето на такса за точка. Ако полето е създадена от редица обвинения, а след това да се изчисли интензивността на този етап е необходимо да се направи рисунка, а след това се определи интензитета като геометричен сбор от интензитета на полетата.

Проблем 1. Две идентични положителен заряд точка намира на разстояние г от друг във вакуум. Определяне на електрически напрегнатост на полето в една точка се намира на същото разстояние R от тези такси.

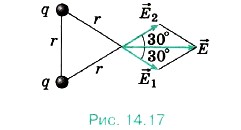
. R е т н д Съгласно принципа на интензивност поле наслагване равна на желаната геометрична сумата от силните страни на полета, генерирани от всяка от такси (фигура 14.17.): = 1 + 2.

Модули силни разходи области са:

Диагонала на успоредник, образуван от векторите 1 и 2 е интензивността на получената област, модула, което е:

Проблем 2. проводим радиус сфера R = 0,2 м, Q за зареждане носител = 1,8 • 10 -4 CI, разположен във вакуум. Определяне на: 1) на модула на електрическото поле на повърхността; 2) 1 единица на интензитета на електрическото поле в точка на разстояние r1 = 10 м от центъра на сферата; 3) интензивност модул 0 в центъра на сферата.

R е т н д. На електрическото поле се зарежда област съвпада с областта на неговата точка на зареждане. следователно

3) напрегнатостта на полето във всяка точка в сферата на провеждане е нула: 0 = Е0.

Проблем 3. еднакво електрическо поле с интензитет Е0 = 3 кН / C има точка заряд р а = 4 • 10 -10 Cl. Определяне на електрически напрегнатост на полето в точка А на разстояние R = 3 cm от заряда на точка. Сегмент свързване на таксата и точка А перпендикулярно на линиите на полето на хомогенна електрическо поле.

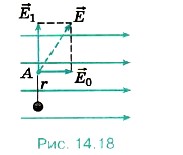
R е с т н д. В съответствие с принципа на суперпозиция, електрическа напрегнатостта на полето в точка А е равна на сумата от вектор интензитет на поле 0 и областта на еднаквото 1. създаден в този момент, без да запазвате електрически заряд. На фигура 14.18 показва тези два вектора и тяхната сума. Според проблема векторите 0 и 1 са взаимно перпендикулярни. Таксата точка на силата на полето

Тогава електрически напрегнатостта на полето в точка А е равна на:

Задача 4. върховете на равностранен триъгълник със странични а = 3 см три такси точка q1 = q2 = 10 -9 CI, q3 = -2 • 10 -9 Cl. Определя силата на тока поле в центъра на триъгълник, в точката О.

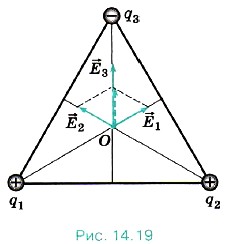
R е т н д Съгласно принципа на суперпозицията на области на напрегнатостта на полето в точката О се равнява на сумата вектор на интензитета на полетата, генерирани от всяко зареждане отделно :. 0 = 1 + 2 + 3. при което освен това

Фигурата показва векторите 14.19 силни 1. 2. 3. Първо, добавете векторите 1 и 2. Както се вижда от фигурата, ъгълът между тези вектори, е равна на 120 °. Следователно, модул модул вектор сума е l1 л и е насочена в същата посока като вектор 3.

Задача 5. Разстоянието между Q1 две фиксирани такси = -2 X 10 -9 Cl и Q2 = 10 -9 m е 1 Cl. В един момент на силата на електрическото поле е равна на нула?

1 и 2, създаден от тези такси, в една и съща посока ">

R е т н д. Очевидно е, че интервалът между напрежението на такси не може да бъде нула, тъй като интензивността на полета 1 и 2. генерирани от тези разходи, в същата посока (фиг. 14,20).

Следователно, напрегнатостта на полето може да бъде нула или надясно или наляво, за обвиненията на линията, минаваща през тези такси.

От първия заряд устройството е по-голям от втория модул, този въпрос трябва да бъде по-близо до второ обвинение, т.е.. Д. В този случай правото на обвиненията. Разстояние от втория заряд на точка А е означена с х. След това при условие, че | "1 | = '2. можем да запишем:

Решаването на това уравнение, получаваме

Задачи за независим решение

1. насочен вертикално надолу еднакво електрическо поле с интензитет на 1.3 • 10 5 N / C капчиците течност маса 2 • 10 -9грама е в равновесие. Определя капчици за зареждане и на броя на излишните електрони върху него.

2. точка заряд Q - 10 -9 Cl заобиколен от сферична черупка на диелектричен с диелектрична константа ε = 2. външната обвивка и вътрешната радиуси са съответно R1 = 5 см и R2 = 6 см Определя интензитет E (R) в електрическото поле. в зависимост от разстоянието от заряда и съставя графика на тези отношения.

3. Три концентрични сфери с радиус R, 2R 3R и мече равномерно разпределени върху техните повърхностни заряди Q1 = + 2q, q2 = -q и Q3 = + р съответно. Известно е, че точка заряд Q в област R на създава електрическо поле с интензитет Е1 = 63 Н / Cl. Каква е силата на полето в една точка, отдалечена от центъра на сферата на разстояние 2,5R?

Проби от работни места УПОТРЕБА

А1. Точка B е в средата на отсечката AC. Фиксирани такси точка и -q -2q с точките А и С, съответно (виж. Фиг.). Каква е таксата трябва да бъде поставен в точка C вместо -2q такса за електрическо интензивността на полето в точка Б се е увеличил през 2 пъти?

1) -5q 2) 4q 3) -3q 4) 3q

C2. Точка заряд Q, поставен в координатна произход, създава точка А на интензивност на електростатично поле ЕА = 65 N / C (вж. Фиг.). Каква е силата на ИБ точка Б?

С3. В еднакъв интензитет на електрическото поле вектор сочи вертикално нагоре, висящи топка с тегло 10гр и таксата от 5 тС. Когато областта е изключен сила на опъване на конеца се повишава два пъти. Определяне на интензитета на полето.