Праволинейно движение на материална точка

Формулите са получени праволинейно движение на задачи три начина на движение - на известни координати, в зависимост от времето; известно ускорение в зависимост от времето и ускоряване на координата. Счита праволинейни еднакво праволинейни равномерно ускорено движение.

Основни формули на праволинейно движение

Нека един материал преминава точка по линията. Освен това, и покаже позицията и скоростта на точката, в началния момент.
Ако промените закона, определени координати на време:
.
разграничаване на координатната от време, ние получаваме от скоростта и ускорението на точка:
;
.

Нека се знае зависимостта на ускорението от време:
.
След това, в зависимост от скоростта и позицията от време на време се определя от формулата:
(1);
(2);
(3);
(4).

Да предположим, че ние знаем, ускорението зависи от координати:
.
След това, зависимостта на скоростта на координатите е както следва:
(5).
координират времето се определя в имплицитна форма:
(6).

За праволинейно равномерно движение:
;
;
.

За праволинейни равномерно ускорено движение:
;
;
;
.

Формулите, дадени тук, могат да се използват не само за праволинейно движение, но и за някои случаи на криволинейни движения. Например, за триизмерно движение в правоъгълна координатна система. ако предложението по оста е независимо от стойностите на прогнози на другите оси. След формули (1) - (6) осигуряват стойности на прогнози в зависимост от оста.

Също така, тези формули са приложими при шофиране по предварително установен маршрут на движение по време на естествения процес на работа. Само тук той действа като координира от дължината на дъгата път измерва от избрания произход. След това, вместо на издатините и трябва да бъдат заменени и - проекция на скоростта и ускорението на избраната посока на допирателната към траекторията.

Праволинейно при известни координати, в зависимост от времето

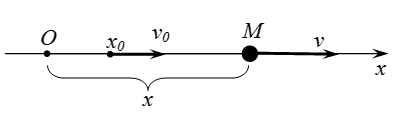
Да разгледаме случая, когато материалната точка се движи по права линия. Ние ще изберем координатната система с неговия произход на произволна точка. Ос е насочена по линията на движение на точка. Тогава положението на точката се определя еднозначно от сингъла координира.

Ако законът се променя зададените координати на време.
.
След това разграничаване по отношение на времето. Ние считаме, степента на промяна на закона:
.
Когато се движи точка в положителна посока (от ляво на дясно на фигурата). Когато се движи точка в отрицателна посока на оста (в цифрата от дясно на ляво).

Разграничаване по отношение на времето на скоростта, ние откриваме, правото на промяна на ускорение:
.
Тъй като линията е без изкривяване, радиусът на кривината на траекторията може да се счита безкрайно голяма. След това, ускорението е равно на нула:






.
Това е точката на тангенциален ускорение (тангенциален)
.
Това е съвсем естествено, тъй като и двете скоростта и ускорението на точка са насочени по допирателна към траекторията - линията, по която се осъществява движението.
Ако същия знак (т.е., както положителни или и двете отрицателни), скоростта на модул увеличава (скорост на повишаване на абсолютна стойност). Ако различни признаци, то модулът намалява скорост (скорост намалява в абсолютна стойност).

Линейно движение с определен ускорение

Ускорение, зависим от времето

Нека се знае правото на промяна на ускорение от време:
.
Нашата задача е да се намери закона на степента на промяна и промяната на координатите на време:
;
.

Нанесете по формулата:
.
Това е първи ред диференциално уравнение с разделящи се променливи. Споделяме променливи и да се интегрират:
;
.
Ето - константата на интеграция. Това показва, че само за известно ускорение в сравнение с времето, не може еднозначно да идентифицира зависимостта на скоростта от време на време. Имаме един куп промени скоростта на закони, които се различават една от друга с произволна константа. За да намерите процент от нас промени закона, ние трябва да поиска още едно значение. Обикновено тази стойност е стойността на скоростта в началния момент. За тази цел се извършва от неопределен интеграл на определението:
.
Да - на мястото на скоростта в началния момент. Ние замени.
;
;
.
По този начин промени закона скорост от време на време има следния вид:
(1).

По същия начин, координатите определят правото на вариация с времето.
.
(2).
Ето - стойността на първоначалното време.

Заместването (1), (2).

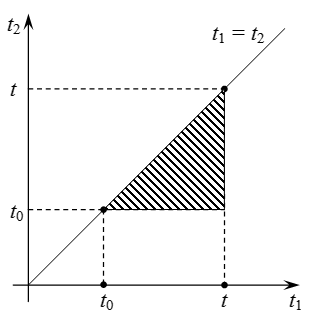
В района на интеграция в двоен интеграл.

Ако промените реда на интеграция в двоен интеграл, получаваме:

По този начин, ние имаме по следната формула:
(3);
(4).

Координатите на ускорение зависим

Да предположим сега, че ние знаем, правото на промяна на ускоряване на координати:
.
Ние трябва да се реши диференциалното уравнение:
.
Това диференциално уравнение не съдържа никаква независима променлива изрично. Общ метод за решаване на тези уравнения се разглеждат на страницата "по-висш порядък диференциални уравнения, които не съдържат независимата променлива изрично." Според този метод, ние вярваме, че е функция на.
;
.
Споделяме променливи и да се интегрират:
;
;
;
.
Като корен квадратен Трябва да се отбележи, че скоростта може да бъде както положителен и отрицателен. На кратко разстояние от точката. знак се определя от знака на константа. Въпреки това, ако ускорението е насочен противоположно на скоростта, скоростта на точка се намалява до нула и посоката на движение е обърната. Затова правилното знак, плюс или минус, е избрана при разглеждането на конкретен движение.
(5).
В началото на движението
.

Сега ние се определи зависимостта на координатите на време. диференциално уравнение на координатите на формата:
.
Това диференциално уравнение с разделящи се променливи. Споделяме променливи и да се интегрират:
(6).
Това уравнение определя зависимостта на координатите на време имплицитно.

Uniform линейно движение

Нека да прилагат посочените по-горе резултати с делото на праволинейното равномерно движение. В този случай, ускорението
.
Според формули (1) и (2) намираме:
;
. Това означава, че скоростта е постоянна, и координира линейна функция на времето. (5) и (6) получаване на същия резултат.

Праволинейни равномерно ускорено движение

А сега да разгледаме праволинейно равномерно ускорено движение.
В този случай, ускорението е постоянно:
.
Според формули (1) и (2) намираме:
;

Ако се прилага с формула (5), ние получаваме зависимостта скорост на координатите:
.

Линейно движение в вектор форма

Получената формула може да бъде представена във вектор форма. За да направите това, умножете достатъчно уравнения, определящи. и единица вектор (единица вектор). насочена по оста.

Тогава радиус вектор от точка, векторите на скоростта и ускорението са от вида:
;
;
.