Как да се изчисли площта на фигурата с помощта на определен интеграл

Начало | За нас | обратна връзка

Ние се пристъпи към разглеждане на молбата на интегралното смятане. В този урок ще разгледаме видовете и най-често срещаният проблем на изчисляване на площта на самолета фигура с помощта на определен интеграл. И накрая, всички търсят смисъл в висша математика - но го намеря. Човек никога не знае. Ще трябва да се подходи живот тук, в крайградски район елементарни функции и да намерят своя район с помощта на определен интеграл.

За да бъде успешно овладяване на материала, трябва да:

1) Запознаване с неопределен интеграл поне на средно ниво. По този начин, кана трябва първо да се запознаят с урока неопределен интеграл. Примери за разтвори.

2) За да могат да прилагат основните теорема формула и изчисляване на определен интеграл. Създаване на топли и приятелски отношения с определени интеграли определен интеграл може да бъде на страницата. Примери за разтвори. Задача ", за да се изчисли площта с помощта на определен интеграл" винаги включва изграждането чертежа. Затова важен въпрос също ще бъде вашият знанията и уменията на конструктивни чертежи. Най-малкото, трябва да сте в състояние да изгради една права линия, парабола и хипербола.

Нека да започнем с извита трапец. Криволинейна трапец - фигура равнина, ограничена от графиката на функция у = е (х), говедото на ос и линии х = А; х = б.

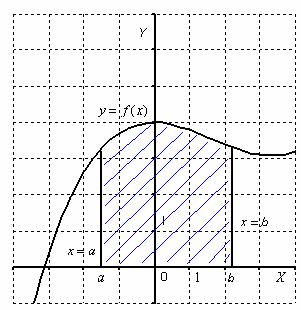
Площта на криволинеен трапец е числено равна на определен интеграл

Всеки определен интеграл (която съществува) има една много хубава геометрична значение. В урока определен интеграл. Примери за решения Казахме, че определен интеграл - този номер. И сега е време да признаем още един полезен факт. От гледна точка на геометрията на определен интеграл от - интервал. Това означава, че определеният интеграл (ако има такъв) геометрично съответства на площта на някои цифри. Помислете за определен интеграл

определя крива в равнината (по желание може да бъде съставен) и определен интеграл е числено равна на площта, съответстваща криволинейна трапец.

Изчислете площта на фигурата, ограничена от линиите. , , ,

Това е типична формулировка на задачата. Най-важният момент на решение - изграждането на чертежа. Освен това, на чертежа трябва да бъдат правилно построена.

В изграждането на рисунката, препоръчвам следната процедура: първо, да се изгради по-добри всички линии (ако има такива), и едва след това - парабола, хипербола, графични и други функции. С изграждането на техника Pointwise могат да бъдат намерени в справочни материали Графики и свойствата на елементарните функции. Там можете да намерите много полезна по отношение на нашия урок - как бързо да се изгради парабола.

През този проблем, решение може да изглежда така.

Извършване на чертеж (обърнете внимание, че уравнението у = 0 определя оста ОХ):

Hatch криволинеен трапец няма да, тук очевидно е, какъв вид площ под въпрос. Решението продължава:

На [-2; 1] графиката на у = х 2 + 2, разположен над osyuOX. Ето защо:

Тези, които имат затруднения с изчисляването на определен интеграл и използване на Нютон-Лайбниц формула

Направете справка с лекция определеният интеграл. Примери за разтвори. След като работата е свършена, винаги е полезно да се вгледате в чертежа и да разбера дали истинският отговор оказа. В този случай, "на око", на броя на клетките в чертежа - добре, около 9 напечатан, подобно на истината. Ясно е, че ако ние се обърна, да кажем, че отговорът е 20 квадратни единици, то е ясно, че някъде грешка - в разглеждания фигурата на 20 клетки явно не е годен, от една дузина сили. Ако отговорът се оказа отрицателен, задачата е също решен правилно.

Изчислява областта на фигурата, ограничена от XY = 4, х = 2, х = 4 и ОХ ос.

Това е пример за независими решения. Цялостни решения и отговори в края на урока.

Какво става, ако криволинеен трапец е под osyuOX?

Изчислява областта на фигурата, ограничена от линиите Y = д - х. х = 1 и координатните оси.

Решение: чертеж:

Ако криволинеен трапец се намира изцяло под оста ОХ. че неговата площ може да се намери чрез формулата:

В този случай:

Внимание! Не бъркайте двата вида проблеми:

1) Ако бъдете попитани за решаване на определен интеграл без геометричен смисъл може да бъде отрицателен.

2) Ако от вас се иска да се намери областта на фигурата с помощта на определен интеграл, районът е винаги положително! Ето защо просто смята формула се появява отрицателен.

На практика често цифра и да се изхвърлят в горната и в долната половина, и следователно, от началното училище zadachek се обърнат към по-смислени примери.

Виж областта на равнина фигура ограничена от линиите у = 2 х - х 2. у = -X.

Решение: Първо, трябва да се извърши на чертежа. В изграждането на рисунката в проблемите в областта ние сме най-заинтересовани от пресечната точка на линиите. Намираме пресечната точка на парабола Y = 2x на - X 2 и права линия у = -х. Това може да стане по два начина. Първият метод - аналитична. Ние решаваме уравнението:

Следователно, долната граница на интеграция, а = 0, горната граница на интеграция б = 3. Най-изгодно и бързо изграждане на линия Pointwise, границите на интеграция се изследва като "себе си". Въпреки това, аналитичен метод за намиране на границите все още понякога трябва да се прилага, ако, например, графиката е достатъчно голяма, или potochennoe конструкция не разкри границите на интеграция (която може да бъде фракционна или ирационално). Ние се върнете към нашата задача: да се изгради рационална първа линия и след това параболата. Извършване на чертеж:

Отново, в сградата на предела Pointwise на интеграция често се изясни "avtomatomaticheski".

Сега работи формула:

Ако интервалът [а; Ь] непрекъсната функция е (х) е по-голямо от или равно на непрекъсната функция г (х), съответната площ на фигурата може да се намери чрез формулата:

Има вече не е необходимо да се мисли, когато фигурата - над оста или под оста, но е важно какво графиката по-горе (по отношение на друго диаграма), и която - по-долу.

В този пример е очевидно, че в интервала [0; 3] парабола се намира над правата линия, и следователно от 2х - х 2 трябва да бъде изваден -х.

Завършване на разтвора може да изглежда така:

Предпочитан фигура ограничена от парабола у = 2 х - х 2 от по-горе и у =-x направо от долу.

В интервала [0; 3] 2х - х 2 ≥ -х. С, съответстваща на формулата:

В действителност, училище формула за областта на извитата трапец в долната половина (виж Пример №3.) - специален случай на формула

Тъй като ОХ ос е дадено от уравнението у = 0, парцел функция ж (х) е разположен под оста ОХ. на

А сега няколко примера за индивидуални решения

Намерете лицето на фигурата, ограничена от

Намерете лицето на фигурата, ограничена от

В хода на решаване на проблеми при изчисляването на района с помощта на определен интеграл се случва понякога забавен инцидент. Рисуване е правилно уреден - Добре, но, по невнимание, ... Намерете областта на грешните цифри.

На следващо място, един истински случай:

Изчислете площта на фигурата, ограничена от линиите. , , ,

На първо място, извършване на чертежа:

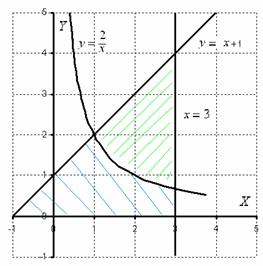
Цифрата, която е област, ние трябва да намерим сенчеста синьо (проверяват внимателно условието - какво цифра е ограничена). Но на практика, поради невнимание, често да реши, че трябва да се намери областта на фигурата, която се сенчести в зелено!

Този пример също е полезна с това, че смята площта на фигурата с две определени интеграли. наистина:

1) на интервала [1; 1] над оста ОХ е линейна графика, у = х 1;

2) на интервала [1; 3] над оста ОХ е хипербола графика у а = (2 / х).

Очевидно е, че зоната може (и трябва) да се добави на, така че:

Изчислете площта на фигурата, ограничена от

Ние представляваме уравнението в "училището", тъй като

и извършване на Pointwise чертеж:

От фигурата става ясно, че горната граница на нашия "добър": б = 1.

Но това, което е най-ниската граница. Ясно е, че това не е цяло число, но какво от това?

Може би, а = (- 1/3)? Но къде е гаранцията, че рисунката е изпълнена с перфектна точност, то може да се окаже, че а = (- 1/4). И ако е погрешно се нанася?

В такива случаи трябва да се харчат допълнително време и да определи границите на интеграция аналитично.

Ние намираме в точката на пресичане на графиките

За да направите това, ние се реши уравнението:

Следователно, = (- 1/3).

Друго решение е тривиално. Основното нещо е да не се губят в замествания и знаци. Изчисленията не са много прости. на интервала

с формула:

В заключение на урока, обърнете внимание на две задачи трудно.

Изчислете площта на фигурата, ограничена от

Решение: Нека си представим, тази цифра в чертежа.

За точка до точка изграждане на рисунката трябва да знаете на външния вид на синусоида. Като цяло, това е полезно да се знае, графиците на всички елементарни функции, както и някои от ценностите на синуса. Те могат да бъдат намерени в таблицата със стойностите на тригонометрични функции. В някои случаи (например този) разрешено изграждането на схематичните фигури, на които по принцип трябва да бъдат показани правилно графика и границите на интеграция.

От външната страна няма никакви проблеми на интеграцията, те следват директно от условието:

- "X" варира от нула до "пее". Ние правим по-нататъшно решение:

В интервала [0; π] графиката на у = грях х 3 се намира над OX оста. Ето защо:

(1) Както е интегрираната синус и косинус в странни сили, че е възможно да видите урока интеграли на тригонометрични функции. Прищипват синусите.

(2) Като се приложи основният тригонометрични идентичност като

(3) извършва промяна на променливата Т = COS х. след това:

Нови етапи на процеса на интеграцията:

Кой прави лоши неща с замествания, моля, преминете към метод клас подмяна в неопределен интеграл. Това не е много ясно, подмяна алгоритъм в определения интеграл, посещение на определен интеграл. Примери за разтвори.

(4) Тук използваме свойствата на определен интеграл

поставяне на граници на интеграция в "обичайните" ред

Изчислете площта на фигурата, ограничена от

Това е пример за независими решения. Цялостно решение и отговорът по-долу.

Помислете за един интересен пример от Arccotangent:

Изчислете площта на фигурата, ограничена от

и координатните оси. Цялостно решение няма. Правилен отговор:

Пример 2: Решение: чертеж:

В интервала [2; 4] графиката на у = 4 / х е разположен над OX ос, следователно:

Забележка: Проблемът с намирането на учителите в тези зони често се налага да записва отговорът е не само точна, но също така и по-специално приблизително.

Пример 5 Решение: чертеж:

В интервала [1; 3]. , с формула:

Пример 6: Решение: Направете чертеж.

В интервала [1; 3] (4-х) ≥ (3 / х), със съответстваща на формулата:

Пример 10: Решение: Ние представляваме тази цифра в чертежа:

На графиката на сегмент се намира над ос. Ето защо:

Забележка: Забележете как интеграла е взета от допирателната в куба, сме използвали основната последица от тригонометрични идентичности

Освен това, в интегралите на метода на сумиране функции под знака на диференциала (може да се използва в замяна на определен интеграл, но решението ще бъде по-дълго).