изометрични

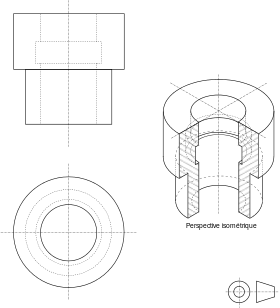
Правоъгълна изометричен изглед на детайли на "ръкава", се извършва въз основа на неговите проекции

Изометричен изглед използван в инженерни и CAD изготвянето на за изграждане на визуални детайли на изображението на чертежа. както и в областта на компютърните игри за триизмерни обекти и панорами.

Трябва да се отбележи, че успоредно проекцията. видове, които са аксонометричен включително изометрична проекция, също разделени в ортогонална (перпендикуляра) на посоката на проекция, перпендикулярна на равнината проекция и допирателната. с ъгъла между посоката и равнина, различна от полето. Според съветски стандарти (вж. По-долу) аксонометрична проекция може да бъде ортогонално и наклонено [1]. В резултат от Западните стандарти изометричен изглед на по-тясно дефиниран и, в допълнение към равенството на скалата на оси, включва състоянието на равни ъгли от 120 ° между всяка двойка издатини на оси. За да се избегне объркване, по-нататък, ако не е указано друго, само правоъгълни изометрична проекция се разбира под изометрична проекция.

Стандартна изометрична проекция на [1] Edit

Правоъгълната (ортогонална) изометрия Редактиране

правоъгълни изометрични аксонометрични оси образуват между тях ъгъл от 120 °, оста Z 'е насочено вертикално. Форма на коефициенти (к х. К у. К Z, k_, k_>) имат цифровата стойност 3 Февруари ≈ 0. 82 >> \ приблизително 0,82>. Обикновено конструкции за улесняване изометричен проекция работи без нарушаване на осите, т.е. изкривяване фактор се определя като 1 в този случай, линейно нарастване на размера на 0. 1 82 ≈ 1. 22> \ приблизително 1,22> пъти.

Наклон по фронталния изометрия Редактиране

Z 'ос е насочена вертикално, ъгълът между оста X' и Z 'равен на 90 °, Y' ос с ъгъл на наклон от 135 ° (120 ° и се оставя до 150 °) от оста Z '.

пред изометричен изглед извършва по осите X ', Y' и Z 'без изкривяване.

Криви успоредни на челната равнина, очаква без изкривяване.

Хоризонтална наклонена изометрия Редактиране

Z 'ос е насочена вертикално, между оста Z' и Y-оста "ъгъл е 120 ° С (135 ° и се оставя до 150 °), при поддържане на ъгъла между осите X 'и Y' равен на 90 °.

Хоризонтална изометрична проекция работи без нарушаване на оси X ', Y' и Z '.

Криви паралелни на хоризонталната равнина [2] се очаква без изкривяване.

Трябва да се отбележи, че тъй като ортогонална тристранен невъзможно да се обърнат, така че две от неговите краища са взаимно перпендикулярни, а третият ръб не се очаква да бъде видими до точка, всички прогнози, която показва всички три оси, но при изготвянето на ъгъла между к -н ​​две - линия (тук това е вторият и третият от по-горе), строго погледнато, в предаването "нещо, което не се случи."

За щастие, че човешкото око е доста успешно поправя тези грешки в представителството на реални обекти, а защото те разрешено за по-голяма простота на строителството на чертежа.

Изометричен изглед на обекта може да се получи от посока на наблюдение, така че ъгълът между проекция ос х. у. и Z са идентични и равна на 120 °. Например, ако вземем куба, то е възможно да се извърши изпращане поглед към един от лицата на куб, след което се обърна на куба ± 45 ° около вертикалната ос и ± arcsin (тен 30 °) ≈ 35,264 ° около хоризонтална ос. Забележка: илюстрация изометрична проекция куб очертае образува правилен шестоъгълник - всички ръбове с еднаква дължина и всички страни на равна площ.

Друг начин да се визуализира изометрична проекция е да се помисли за формата с кубична стая горен ъгъл с посоката на погледа в противоположна долен ъгъл. Х-оста е насочено диагонално надолу и надясно, оста Y - нагоре - надолу и диагонално наляво, Z ос. Дълбочината е отразено и в разгара на изображението. Линиите, начертани по оси имат ъгъл от 120 ° между тях.

Има 8 различни опции за получаване на изометричен изглед, в зависимост от това, което изглежда ъгломер наблюдател. Изометричен трансформация буква а х. у. Z> в триизмерното пространство до точка б х. Y> равнина, когато се гледа в първата октант може да бъде математически описан от матрица въртене, както следва. На първо място, както е обяснено в раздел визуализация. извършва завъртане около хоризонтална ос (тук, х) при α = arcsin (тен 30 °) ≈ 35 264 ° и около вертикална ос (тук, у) на β = 45 °:

Останалите седем възможни видове получава завой за противниковата страна и / или обръщането на посоката на погледа. [3]

Предвид ограничения перспектива Редактиране

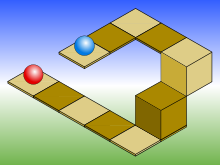
Изометрично рисунка със синя топка на две нива над червения

Както и при други видове паралелни проекции. обекти в перспектива, не изглеждат по-големи или по-малки и при увеличение или далеч от наблюдателя. Това е полезно в архитектурни чертежи и удобно в спрайт ориентирани компютърни игри. но, за разлика от обещаващите (централно) проекцията. Това води до чувство на кривина, както човешкото око или снимка работата по различен начин.

Също така е лесно да доведе до ситуации, при които дълбочината и височината не могат да бъдат оценени, както е показано на илюстрацията вдясно. Това изометрично рисуване синя топка на две нива над червеното, но това е невъзможно да се види, ако се гледа само в лявата половина на изображението. Ако проекцията на която синята топка, да разшири един квадрат, а след това ще бъде точно до площада, който е червена топка, като създава оптична илюзия. ако двете топки на същото ниво.

Допълнителен проблем специфичен за изометрична проекция - трудността за определяне коя страна на обекта наблюдава. При липсата на сенки и за обекти, които са относително перпендикулярно и пропорционална, че е трудно да се определи коя е отгоре, отдолу или отстрани. Това се дължи на приблизително равни по размер и площ от проекции на обекта.

Повечето съвременни компютърни игри го избягват поради изглед без перспектива в полза на дългосрочен триизмерен рендиране. Въпреки това, работата на прожекционни оптични илюзии най-популярните в областта - като например работата на серия от "невъзможно архитектура" Ешер. Falls (1961) - добър пример, в който структурата е главно изометрия, докато се стопи фона използва перспектива прогнози. Друго предимство е, че при изготвянето дори начинаещи може лесно изграждане на ъгли от 60 °, използвайки само началник и компас.

Изометрично проекция във видео игри и пиксел арт Редактиране

Фигура телевизия в почти изометрична пиксел арт. В модела на пикселите е видимо за пропорция 2: 1

В областта на компютърните игри и изглед пиксел арт гледна точка е много популярен поради лекотата, с която на двуизмерни спрайтове и теракота графики могат да се използват за представяне на триизмерна игра среда - както по време на движението на игралното поле обекти не променят размера на компютъра не се изисква да мащабирате спрайтове или за извършване на изчисленията, необходими, за да се симулира визуален перспектива. Това позволи на старите 8-битови и 16-битови системи за игри (и по-късно, преносими системи за игри), за да лесно да показват голяма триизмерното пространство. Въпреки объркване с дълбочина (вж. По-горе), понякога може да се окаже проблем, добра игра дизайн е в състояние да го смекчи. С появата на оглед по-мощни графични системи перспектива започва да губи своите позиции.

Проекцията на компютърни игри обикновено е малко по-различен от "истинска" гледна точка, поради ограниченията на растерна графика - линии на Х и У осите няма да има чист пиксел модел ако изготвен под ъгъл от 30 ° спрямо хоризонталата. Въпреки че съвременните компютри могат да решат този проблем чрез изглаждане. ранните компютърна графика не подкрепят достатъчно цветова палитра, или не разполагат с достатъчно процесорна мощ, за да го стартирате. Вместо да използва част от модела на пикселите от 2: 1 за равен на осите х и у. при което тези оси, разположени под ъгъл arctg 0,5 ≈ 26 565 ° спрямо хоризонталата. (Игра системи с не-квадратни пиксели обаче може да доведе до други ъгли, включително напълно изометричен [4]). Както тук от трите ъгъла между осите (116.565 °, 116.565 °, 126.87 °) равни само две такъв вид проекция по-точно характеризира като вариант dimetric проекция. Въпреки това, по-голямата част от общността на компютърните игри и растерна графика продължава да наричаме тази проекция "изометрична перспектива". Също така, често се използва терминът "тип 3/4 (инж.)," А "2.5D".

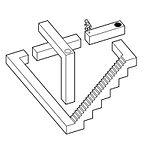
Изстрел на играта «echochrome»

Интересен пример за използването на функциите, наблюдавани в изометричен изглед на игра echochrome (японец 無限 回廊 Mugen Кайро :.). Мотото на играта - "В този свят, какво виждаш, се превръща в реалност." Смисълът на играта е, че илюзията, възниква при разглеждането на триизмерно изометрични построен ниво с определена точка, престава да бъде една илюзия. Например, ако се вгледате в нивото, така че обектите, намиращи се на различни височини, изглеждаше така, сякаш те са на същата височина (см. Изображение с червени и сини топки в предишния раздел), играта ще се счита, че е в на същата височина, както и на лицето (на играча) може лесно да "прекрачи" от едно място на друго. След това, ако включите на нивото на картата и погледнете структурата, така че да се вижда ясно разликата във височината, тя може да се разбере, че в действителност човек "излезе" на различна височина, като се използва факта, че изометрични илюзия в някакъв момент да се превърне в реалност. Фигурата като илюстрация на рамката на играта сайт ситуация, разположен в горната част на стълбата, може да се представи по два начина: в един случай е на същото ниво като платформата, на която играчът (може да надхвърли), а в друг случай - под нея (възможно е да скочи през черна дупка). И двата случая едновременно ще бъдат верни. Очевидно е, че този ефект се постига чрез липсата на перспективи в перспектива.

История на изометрични компютърна игра Edit

Q * BERT (1982), една от първите игри с изометрични графики

Първите игри, използващи изометрия, аркадни игри са били в началото на 1980-те години: това е така, Q * BERT [11] и Zaxxon (на английски език.) [12], издаден през 1982. Q * BERT показва статичен пирамида, изготвен в изометрична перспектива, в която играчът трябва да скочи контролирани характер. Zaxxon предлага скролируеми изометрични нива, над които лети играч контролирани самолет. Една година по-късно, през 1983 година. аркада игра Конго Бонго (Eng.) е била освободена [13]. Тя работи на същите слотове като Zaxxon. В тази игра характер движи в голям изометрични нива, включващи триизмерни изкачвания и спускания. Същото се предлага в аркадна игра Marble Madness на (1984 г.).

• Богданов VN Malezhik I. Е. Verkhola AP, и др. Референтен изчертаване. - М. машиностроене, 1989 - S. 864. - ISBN 5-217-00403-7.
• Frolov S. A. Дескриптивна геометрия. - 2-ро издание. Ревизираната. и вътр. - М. машиностроене, 1983 - С. 240.