Изчисляване области на равнинни фигури използват интеграли
В този урок ще се научим да се изчисли площта на равнинни фигури. които са ограничени от оста на абсцисата (Ox), прави сегменти линия х = а. х = б, и графика на непрекъснат и неотрицателна функция у = е (х) за стойности на "Х" в интервала [а. Ь]. Това число се нарича криволинеен трапец. Странични сегменти може да се изроди до точка. S на този размер криволинейна трапец може да бъде изчислена по формулата
По този начин, определен интеграл на неотрицателно непрекъсната функция е (х) на [а. Ь] (функция графика намира над оста Ox) е числено равна на площта на кривата трапец с основа [а. Ь]. графика, ограничена по-горе функция у = е (х). Това е геометрична смисъла на определен интеграл. Чертежи на фигури - в примерите.
Ако е (х) ≤ 0 (функция графика е разположен под оста Ox), областта на извитата трапец може да бъде изчислена по формулата
Все още има случаи, когато двете горни и долни граници на фигурата - функция, съответно, у = F (х) и у = φ (х). областта на фигурата изчислява по формулата
По този начин, изчисляването на областите на равнинни фигури - един от най-важните приложения, в които определеният интеграл е най-ползотворно приложение. Всички ние разгледахме данни от елементарна геометрия, която позволява да се изчисли площта на праволинейни фигури - правоъгълници, триъгълници и многоъгълници. Що се отнася до извити форми, има за намиране областта на средства за елементарна геометрия вече не е достатъчно. Така че, за работа. Научете как да приложите това, което е посочено в горната част на тази статия.
Ние започваме с случаите, когато площ на фигурата може да се изчисли чрез формулата (1).
Пример 1. търсене площ на фигурата, ограничена от функцията график на абсцисата (Ox) ос и правите линии х = 1. х = 3.
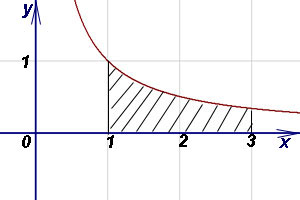
Решение. Тъй като у = 1 / х> 0 в интервала [1; 3]. областта на криволинейна трапец открити по формула (1):
Пример 2. Виж областта на фигурата, ограничена функция графика линия х = 1, и оста на абсцисата (Ox).
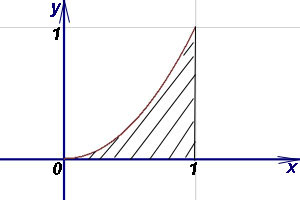
Решение. Съгласно формула (1), имаме
Ако S = 1/2; ако това е = 1/3. и т.н.
Пример 3. Виж областта на фигурата, ограничена от функцията на график, оста на абсцисата (Ox) и една права линия х = 4.
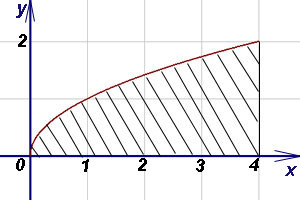
Решение. Вие фигура - криволинеен трапец, който напусна сегмент дегенерира до точката. ограничения интеграция са 0 и 4. Тъй като, съгласно формула (1) намери областта на криволинейна трапец:
Пример 4. Намерете областта на ограничена от линиите, и се намира в 1-ви квадрант фигурата.
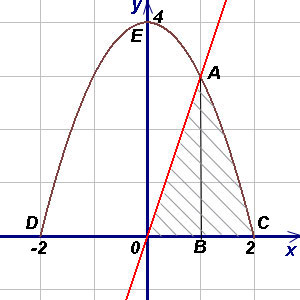
Решение. За използване на формула (1) представляват областта на желаната форма под формата на сумата от площите на триъгълници ОАВ и криволинейна трапец ABC. При изчисляване на площта на триъгълник ОАВ граници интеграция са абсциси на О точки и A. фигури и за ABC - абсциса на точките А и С (А е пресечната точка на параболата и правата линия, OA, и С - точката на пресичане с параболата ос Ox). Решаването (като система) на права линия и парабола, ние получаваме (абсциса точка А) и (абсциса на другата точката на пресичане на права линия и парабола, която не е необходима за вземане на решение). По същия начин, ние получаваме (абсцисата точки В и D). По този начин, ние имаме всичко, за да се намери областта на фигурата. ние намираме:
Пример 5. Намерете областта на криволинеен трапец ACDB. ако уравнението на CD крива и абсциса А и В, съответно, 1 и 2.
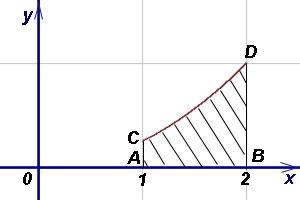
Решение. Експресна чрез уравнението на у крива: Площ криволинейна трапец открити по формула (1):
Обръщаме се към случаите, когато площта на фигурата може да се изчисли от формула (2).
Пример 6. Виж областта на фигурата, ограничена от парабола и оста на абсцисата (Ох).
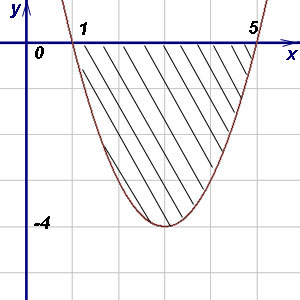
Решение. Тази цифра се намира под оста х. Ето защо, за да се изчисли неговата зона на използване (2). Границите на интеграция са абсцисата и пресечните точки с параболата ос Ox. Ето защо,
Пример 7. Виж областта, затворена между оста на абсцисата (Ox) и двете съседни задължително вълни.
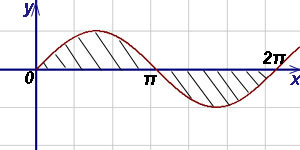
Решение. Площта на тази фигура може да се намери с формула (2):
Нека да се намери всеки термин:
Най-накрая се намери района:
Пример 8. Намерете лицето на фигурата, и сключен между кривата на парабола.
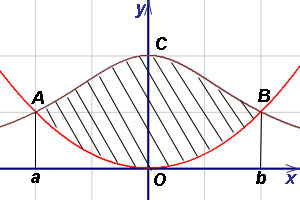
Решение. Ние изрази линия уравнение по отношение на Y:
Площ под формула (2) как да се получи
където А и Б - абсциса на точки А и Б. Ние ги намерите, решаване на уравнения:
Най-накрая се намери района:
Накрая, в случаите, когато площта на фигурата може да се изчисли от формула (3).
Пример 9. Виж областта на фигурата, ограничена от графиките на функции и директен и.
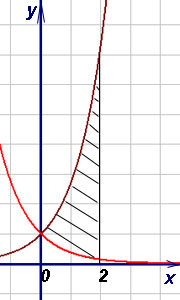
Решение. Тъй интервала [0, 2]. След това, като се използва формулата за намиране на областта (3), получаваме
Пример 10. Намерете лицето на фигурата, и сключен между параболи.
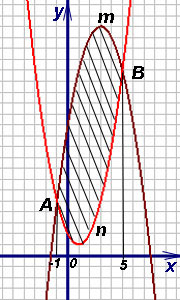
Решение. AMBN необходимо да се изчисли площта на фигурата. в който страничните сегменти дегенерирали в точка А и параболи на пресичане B. Решаването (както се изисква) парабола уравнение, ние откриваме тяхната абсциса и. В интервала [1, 5] получаваме. Затова формулата (3) намираме областта на фигурата:
Пример 11. Намерете лицето на фигурата, сключен между парабола и една права линия.
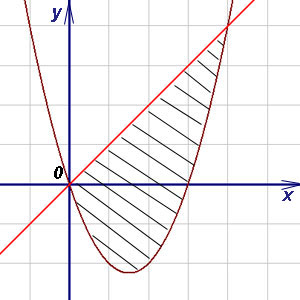
Решение. Намираме абсцисата на точки на пресичане на парабола и една права линия и. Тъй интервала [0, 4]. формулата (3) намираме областта на фигурата: