Изчисляване на площ с предварително определена неразделна
Ние се пристъпи към разглеждане на молбата на интегралното смятане. В този урок ще разгледаме видовете и най-често срещаният проблем - как да се използва определеният интеграл да се изчисли площта на самолета фигура. И накрая, търсейки смисъл в висша математика - но го намеря. Човек никога не знае. Ще трябва да се подходи живот тук, в крайградски район елементарни функции и да намерят своя район с помощта на определен интеграл.
За да бъде успешно овладяване на материала, трябва да:
1) Запознаване с неопределен интеграл поне на средно ниво. По този начин, кана трябва първо да се запознаят с урока неопределен интеграл. Примери за разтвори.
2) За да могат да прилагат основните теорема формула и изчисляване на определен интеграл. Създаване на топли и приятелски отношения с определени интеграли определен интеграл може да бъде на страницата. Примери за разтвори.
В действителност, да се намери областта на фигурата не е необходимо да има много познания за неопределен и определен интеграл. Задача ", за да се изчисли площта с помощта на определен интеграл" винаги включва изграждането чертежа. много по-важен въпрос, ще ви бъде знанията и уменията на конструктивни чертежи. В тази връзка е полезно да се реша на основни графики на елементарни функции, и, като минимум, да може да се конструира по права линия, парабола и хипербола. Това може да стане (много - необходимо) с помощта на методически материали Графики и свойства на елементарни функции и членове на геометрични трансформации на графики.
Всъщност, с задачата за намиране на района с помощта на определен интеграл всички Познаваме се още от гимназията, и да си тръгнем малко по-напред от учебната програма. Тази статия по принцип не би било, но факт е, че проблемът се появява в 99 от общо 100 случая, когато един студент страда от омразния кула ентусиазъм усвояване курс на висшата математика.
Известия на семинара са изложени просто, в детайли и с най-малко теория.
Нека да започнем с извита трапец.
Извита трапец нарича равнина фигура, ограничена от оста, прав и интервал график непрекъсната функция, която не се променя знак в този интервал. Нека не тази цифра е под х-ос:
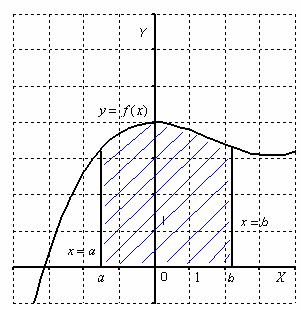
Тогава областта на криволинеен трапец е числено равна на определен интеграл. Всеки определен интеграл (която съществува) има една много хубава геометрична значение. В урока определен интеграл. Примери за решенията, казах, че определен интеграл - този номер. И сега е време да признаем още един полезен факт. От гледна точка на геометрията на определен интеграл от - интервал.
Това означава, че определеният интеграл (ако има такъв) геометрично съответства на площта на някои цифри. Помислете например за определен интеграл. В подинтегрален определя равнинна крива, която се намира над оста (всеки може да се изпълнява на чертежа), а определеният интеграл е числено равна на площта, съответстваща криволинеен трапец.
Изчислете площта на фигурата, ограничена от ,,,.
Това е типична формулировка на задачата. Първият и най-важен момент решения - изграждане рисуване. Освен това, на чертежа трябва да бъдат правилно построена.
В изграждането на рисунката, препоръчвам следната процедура: първо, да се изгради по-добри всички линии (ако има такива), и едва след това - парабола, хипербола, графични и други функции. Графики функции изгодно да се изгради Pointwise. с уреди Pointwise строителство могат да бъдат намерени в справочни материали Графики и свойствата на елементарните функции. Там можете да намерите много полезна по отношение на нашия урок - как бързо да се изгради парабола.
През този проблем, решение може да изглежда така.
Извършване на тираж (имайте предвид, че уравнението определя оста):
Аз няма да се излюпят криволинеен трапец, това е очевидно от някои райони става въпрос. Решението продължава:
На графиката на сегмент се намира над ос. Ето защо:
Тези, които имат затруднения при изчисляването на определен интеграл и използване на Нютон-Лайбниц формула, вижте лекцията определен интеграл. Примери за разтвори.
След като работата е свършена, винаги е полезно да се вгледате в чертежа и да разбера дали истинският отговор оказа. В този случай, "на око", на броя на клетките в чертежа - добре, около 9 напечатан, подобно на истината. Ясно е, че ако ние се обърна, да кажем, че отговорът е 20 квадратни единици, то е ясно, че някъде грешка - в разглеждания фигурата на 20 клетки явно не е годен, от една дузина сили. Ако отговорът се оказа отрицателен, задачата е също решен правилно.
Изчислете площта на фигурата, ограничена от линиите, а оста
Това е пример за независими решения. Цялостни решения и отговори в края на урока.
Какво става, ако криволинеен трапец се намира под оста?
Изчислете площта на фигурата, ограничена от линии, както и координатните оси.
Решение. Извършване на чертеж:
Ако извити трапец разположен под оста (или поне не по-висока от даден ос), площ може да се намери чрез формулата:
В този случай:
Внимание! Не бъркайте двата вида проблеми:
1) Ако бъдете попитани за решаване на определен интеграл без геометричен смисъл може да бъде отрицателен.
2) Ако от вас се иска да се намери областта на фигурата с помощта на определен интеграл, районът е винаги положително! Ето защо просто смята формула се появява отрицателен.
На практика често цифра и да се изхвърлят в горната и в долната половина, и следователно, от началното училище zadachek се обърнат към по-смислени примери.
Намери равна площ на фигурата, ограничена от линии.
Решение. Първо трябва да се извърши на чертежа. Най-общо казано, изграждането на рисунката в проблемите в областта ние сме най-заинтересовани от пресечната точка на линиите. Ние намираме в точката на пресичане на парабола и една права линия. Това може да стане по два начина. Първият метод - аналитична. Ние решаваме уравнението:
Следователно, долната граница на интеграция, горната граница на интеграция.
По този начин по-добре, за да не се възползва от възможността.
Тя е много по-изгодно и по-бързо да се изгради линия от точка-мъдър, и границите на интеграция са установили, така да се каже "сами по себе си." Техника Pointwise конструкция за различни графики разгледани подробно в модели на Графиките и свойства на елементарни функции. Въпреки това, аналитичен метод за намиране на границите все още понякога трябва да се прилага, ако, например, графиката е достатъчно голяма, или potochennoe конструкция не разкри границите на интеграция (която може да бъде фракционна или ирационално). И този пример, ние също се разгледа.
Ние се върнете към нашата задача: да се изгради рационална първа линия и след това параболата. Извършване на чертеж:
Отново, когато изграждането на границите Pointwise на интеграция често се срещат от "автоматично".
Сега работи формула. Ако интервалът непрекъсната функция е по-голямо от или равно на непрекъсната функция, областта на фигурата, ограничена от графиките на функции и данни линии, може да се намери от формулата:
Там вече не трябва да се мисли, когато фигурата - над оста или под оста, и, грубо казано, важно е това, което на графиката по-горе (по отношение на друго диаграма), и която - по-долу.
В този пример се вижда, че параболата на сегмент се намира над правата линия, и по този начин трябва да се изважда от
Завършване на разтвора може да изглежда така:
Вие фигура, ограничена от парабола и една права линия от горе до долу.
В интервала на съответната формула:
В действителност, училище формула за района на извитата трапец в долната половина (виж прост пример №3.) - специален случай на формула. Тъй като е дефинирано по уравнението ос, графика на функцията не се намира над ос,
А сега няколко примера за индивидуални решения
Намерете лицето на фигурата, ограничена от линии.
Намерете лицето на фигурата, ограничена от линии.
В хода на решаване на проблеми при изчисляването на района с помощта на определен интеграл се случва понякога забавен инцидент. Рисуване е правилно уреден - Добре, но по невнимание намери района ... не тази цифра. по този начин няколко пъти разхвърлян уважение. Ето събитие от реалния живот:
Изчислете площта на фигурата, ограничена от ,,,.
Решение. На първо място, извършване на чертежа:
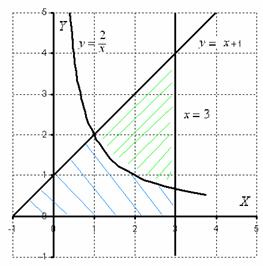
... О, hrenovenky рисунка излезе, но изглежда, че все още четливи.
Цифрата, която е област, ние трябва да намерим сенчеста синьо (проверяват внимателно условието - какво цифра е ограничена). Но на практика често има липса на внимание на "бъг", който трябва да намери площ от фигурата, която се сенчести в зелено!
Този пример все още е полезен с това, че смята площта на фигурата с две определени интеграли. наистина:
1), разположени на сегмент над оста на линейната графика;
2) В сегмента над ос на графиката е хипербола.
Очевидно е, че зоната може (и трябва) да се добави на, така че:
Ние се обръщаме към един по-смислен задача.
Изчислете площта на фигурата, ограничена от линиите,
Представлява уравнение формата на "училище", и да изпълни Pointwise чертеж:
От фигурата става ясно, че горната граница на нашата "добра" :.
Но това, което е най-ниската граница. Ясно е, че това не е цяло число, но какво от това? Може би? Но къде е гаранцията, че рисунката е изпълнена с перфектна точност, то може да се окаже, че. Или корен. И ако е погрешно се нанася?
В такива случаи трябва да се харчат допълнително време и да определи границите на интеграция аналитично.
Намираме пресечните точки на линията и параболата.
За да направите това, ние се реши уравнението:
,
Друго решение е тривиално, по-важното е, да не се губят в замествания и знаци, изчисление не е много проста.
В интервала на съответната формула:
Е, в заключение на урока, обърнете внимание на две задачи трудно.
Изчислете площта на фигурата, ограничена от линиите,
Решение. Ние представляваме тази цифра в чертежа.
По дяволите, забравих да подпише график, но да ремонтирам на картината, съжалявам, не Hotz. Не чертежа, с една дума, днес е денят =)
За точка до точка изграждането на необходимост да се знае появата на задължително вълна (и по принцип е полезно да се знае разписанията на всички елементарни функции), както и някои от стойностите на синус, те могат да бъдат намерени в тригонометрични масата. В някои случаи (като този) е позволено да се изгради най-схематични чертежи, в които по принцип трябва да бъдат показани правилно графика и границите на интеграция.
От външната страна няма никакви проблеми на интеграцията, те следват директно от състоянието: - "X" варира от нула до "пикая". Ние правим по-нататъшно решение:
На графиката на сегмент се намира над оста, така че:
(1) Както е интегрираната синус и косинус в странни сили могат да бъдат намерени в урока интеграли на тригонометрични функции. Този идиом, отщипвам синусите.
(2) Като се приложи основният тригонометрични идентичност като
(3) да извърши промяната на променливи, тогава:
Новите граници на интеграция:
Кой прави лоши неща с замествания, моля, преминете към метод клас подмяна в неопределен интеграл. Това не е много ясно, подмяна алгоритъм в определения интеграл, посещение на определен интеграл. Примери за разтвори.
(4) Тук използваме свойствата на определен интеграл, при определени лимити на интеграцията в "обичайните" ред
Изчислете площта на фигурата, ограничена от линиите,
Това е пример за независими решения. Цялостно решение и отговор на партерния етаж.
Тук, може би, както и всички основни техники за намиране на място. Освен техниките на интеграция, понякога е необходимо да се прилага формулата за интегриране по части в определен интеграл, това не е особено затруднение. Някои интересен пример да се мисли усилено ... все пак ... дъга котангенс вид никога не са изпълнени:
Изчислете площта на фигурата, ограничена от линии, както и координатните оси.
Цялостно решение не е необходимо, тъй като вие сте малко по-трудно. А верен отговор ще кажат. Всички необходими материали за работата на сайта е! ;-) И още повече - след три дълги години, най-накрая се появи изчисляването на статия зона в полярни координати, както и изчисляването на повърхността, ако линията се определя по параметри.
Решения и отговори:
Пример 2: Разтвор:
Извършване на чертеж:
На графиката на сегмент се намира над оста, така че:
отговори на:
Забележка: Проблемът с намирането на учителите в тези зони често се налага да записва отговорът е не само точна, но също така и по-специално приблизително.
Пример 10: Разтвор:
Ние представляваме тази цифра в чертежа:
На графиката на сегмент се намира над оста, така че:
отговори на:
Забележка: Забележете как интеграла е взета от допирателната в куба, сме използвали следствие основни тригонометрични идентичност. Освен това, в интегралите аз използвах метода на сумиране функции по диференциално знак (може да се използва за замяна на определен интеграл, но решението да се получи дълго). Ако срещнете трудности с тези интеграли, интеграли посещават урока на тригонометричните функции.
(Към началната страница)
работа Качество без плагиатство - Zaochnik.com