Функция зона и редица примери на функции
основен Nbsp> Nbsp страница-Упътване Nbsp> Nbsp математика Nbsp> nbsp9 клас Nbsp> nbspFunktsiya: домейни и диапазон стойности на функции + ПРИМЕРИ
Функцията е модел. Ние дефинираме X, набор от стойности на независимата променлива // независим -Така такива.
Функцията е правило, с което всяка стойност на независимата променлива в комплект X могат да бъдат намерени само зависимата променлива. // т.е. за всеки х има един край.
Определението предполага, че има два ponyatiya- независима променлива (който е обозначен с х и може да приеме всяка стойност) и зависимата променлива (който е обозначен с Y или F (х) и се изчислява от функция когато заменен х).
1. The Independent е х, тогава се взема никаква стойност, нека х = 3
2. Сега и изчислителна у, тогава Y = X = 5 + 5 + 3 = 8. (В зависимост от х, защото заместител X, Y, и така получаваме)
Казват, че променливата у е функционално зависи от променливите х, и се означава, както следва: у = е (х).
2. у = х ^ 2. (Наречен. Парабола)
3.u = 3 + 7. (Т.нар. Line)
4. у = √ х. (Наречен. Парабола клон)
Независимата променлива (кат. Ще означаваме х) е името на аргумента на функцията.
В областта на функцията
Наборът от стойности, измерени чрез аргумент функция, наречена домен на определение на функцията и е означен с D (е) или D (у).
Да разгледаме D (у) за 1., 2., 3, 4.
1. D (у) = (∞ 0) и (0 + ∞) // определя всички реални числа с изключение на нула.
2. D (у) = (∞ + ∞) // всички множествено deystvit.chisel
3. D (у) = (∞ + ∞) // всички множествено deystvit.chisel
4. D (у) = [0; + ∞) // млн на neotritsat.chisel
Зависимата променлива (кат. Означаваме у) е името на стойността на функцията.
Полеви стойности на
Наборът от всички стойности, които могат да зависимата променлива, наречена домен на стойности на функцията и е означен с E (е) или E (Y).
Помислете E (Y) за 1, 2, 3, 4.
1. Е (у) = (∞ 0) и (0 + ∞) // определя всички реални числа с изключение на нула.
2. Е (у) = [0; + ∞) // млн на neotritsat.chisel
3. Е (у) = (∞ + ∞) // всички множествено deystvit.chisel
4. E (у) = [0; + ∞) // млн на neotritsat.chisel
Помислете примерите по-
1) Изявление на проблема. Виж функция у = 4 / (3 + х)
1. търсене D (където Y) // т.е.. Кои стойности могат х. за тази цел, ние откриваме, TCC (фракция гама от допустимите стойности)
означава D (у) на функцията (∞ 3) и (3 + ∞) // определя всички реални числа, различни от три.
2. търсене E (у) // т.е.. Какви ценности може да има, за всички възможни х
решаване на уравнение на формата на 4 / (3 х +) = А, където А Je E (у)
Това означава, E (у) на функцията (∞ 4) и (4 + ∞) // определя всички реални числа, различни от четири.
2) Изявление на проблема. Виж D (у) и Е (у) на функцията е показано на графиката
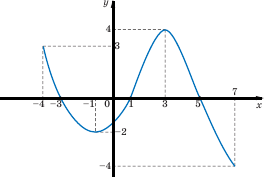
определение поле (стойност на х) е вид на интервала на оста х [4; 7]
стойности домейни (у стойности) търсят у е количеството на [4; 4].