Електрически векторно поле 1

В съответствие с теорията на къси разстояния, взаимодействия между заредените органи, които са отдалечени един от друг, носени от полета (електромагнитни), произведени от тези органи в околното пространство. Ако полетата са фиксирани частици (органи), електростатичното поле е. Ако не се променя терена във времето, той се нарича неподвижна. В електростатично поле е неподвижен. Това поле - частен случай на електромагнитното поле. характеристика на мощност на вектора на електрическа сила на полето се използва, което може да бъде дефинирана като:

където $ \ overrightarrow $ - ". изпитване" е силата, приложена от областта на неподвижно заряд Q, който понякога се нарича По този начин е необходимо да се "тест" такса е малка, така че да не нарушава областта, чиято интензивност се измерва го използвате. От уравнение (1) показва, че напрежението съвпада с посоката на силата, с която областта действа върху единица положителен "тест заряд" на.

електрически интензитет на поле не зависи от времето. Ако интензивността на всички места за едни и същи, областта се нарича хомогенна. В противен случай, полето не е еднаква.

силовите линии,

За графично представяне на електростатично поле с помощта на концепцията за силови линии.

Силови линии или поле интензитет линии се наричат ​​линии, чиито допирателни във всяка точка на областта съвпада с посоката на напрежение на тези точки.

Силовите линии на електростатичното поле са тази позиция. Те започват на положителни заряди и приключи на отрицателна. Понякога те могат да отидат до безкрайност или идват от безкрайност. Линиите на полето не се пресичат.

Векторът на електричното поле се подчинява на принципа на суперпозиция, а именно:

Получената поле вектор може да се намери като вектор сумата от напрежението на неговите "индивид" области. Ако таксата е разпределена непрекъснато (не е необходимо да се вземат предвид дискретността), сумарната напрегнатост на полето съществува като:

В уравнение (3), интегрирането се извършва по площта на разпределението на заплащане. Ако обвиненията се разпределят по ред ($ \ тау = \ Фрак $ линейна плътност на разпределението на заплащане), интегрирането в (3) се извършва по линията. Ако обвиненията се разпределят по повърхността и повърхностната плътност на разпределението на $ \ сигма = \ $ Фрак, а след това се интегрират над повърхността. Интеграцията се извършва върху силата на звука, ако сделката с разпределението на пространството такса: $ \ р = \ Фрак $, където $ \ р $ - обем плътност на разпределението на заплащане.

напрегнатостта на полето

напрегнатостта на полето в изолатора е равна на сумата от вектор интензитета на полетата, които създават свободни такси ($ \ overrightarrow $) и свързаните с тях разходи ($ \ $ overrightarrow):

Много често в примерите сме изправени пред факта, че диелектрик е изотропно. В този случай, интензивността на полето може да се запише като:

където $ \ varepsilon $ - относителна диелектрична константа на средата в даден момент на терена. Така, от (5), че в хомогенна изотропно диелектрична якост на електрическото поле в $ \ varepsilon $ пъти по-малко, отколкото във вакуум.

Интензитетът на електростатичното поле на точка обвинения в системата е:

В напрежение система областта точка зареждане на CGS във вакуум е равна на:

Задача: Обвинението е равномерно разпределена над една четвърт окръжност с радиус R, с линейна плътност $ \ тау $. Намери напрегнатостта на полето в точката (A), което би било централния кръг.

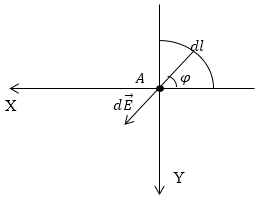
Различаваме върху наелектризираната част от обиколката на елементарни част ($ дл $), която ще се създаде елемент в точка А, за да напише израз за това сила (CGS ще използва системата), а след това на израза за $ г \ overrightarrow $ има следния вид:

Прожекция на $ г \ overrightarrow $ по оста ОХ е в следния формат:

Ние изразяваме DQ чрез линейна плътност такса $ \ тау $:

\ [DQ = \ тау дл = \ тау \ cdot 2 \ пи RDR \ \ наляво (1.3 \ дясно). \]

Използването на (1.3) ние се трансформира (1.2), получаваме:

където $ 2 \ пи DR = г \ varphi $.

Намираме пълна проекция $ E_x $, интегриране (1.4) над $ г \ varphi $, където ъгълът се променя $ 0 \ ле \ varphi \ ле 2 \ пи $.

Нека проекция интензивност вектор на оси OY, по аналогия, без никакви специални обяснение можем да запишем:

\ [_ Y = dEsin \ varphi = \ fracsin \ varphi г \ varphi \ \ наляво (1.6 \ дясно). \]

Интегриране на израза (1.6), ъгълът се променя $ \ Фрак \ ле \ varphi \ ле 0 $, получаваме:

Ние считаме, големината на интензитета в точка А, с помощта на питагорова теорема:

Отговор: напрегнатостта на полето в точката (A), се равнява на $ E = \ Фрак \ SQRT $ на.

Цел: Намерете електростатичното поле е равномерно заредена полукълба, чийто радиус е равен на R. плътност повърхностен заряд е равен на $ \ сигма $.

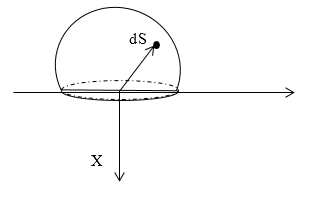
Изолират на повърхността на заредена сфера начално зареждане $ DQ $, която е разположена върху площ елемент $ $ DS В сферична координира $ $ DS е .:

\ [DS = R ^ 2sin \ тета г \ тета г \ varphi \ \ наляво (2.1 \ полето), \]

където $ 0 \ ле \ varphi \ ле 2 \ пи \ 0 \ ле \ тета \ ле \ Фрак. $

Ние пишете израза за начално точка на напрегнатостта на полето такса в SI:

Vector напрежение дизайн на ОХ ос, получаваме:

Начално зареждане изразена по отношение на плътността на повърхностния заряд, получаваме:

\ [DQ = \ сигма DS \ \ ляво (2.4 \ дясно). \]

Ние замести (2.4) в (2.3), като се използва (2.1) Интегриране, получаваме:

Лесно е да се получи, че $ E_Y = 0. $

А :. напрегнатостта на полето на заредени полукълбо повърхността в центъра е $ E = \ frac_0> $