1 напрежение линии
§2.1 напрежение линии. Потока интензитет вектор.
На електрическото поле е еднозначно определена, ако величината (модул) и посоката на вектора за всяка точка от пространството. Това може да стане, ако в пространството за провеждане на така наречения напрежение линия (електропровод) в електрическо поле.
Тези линии са съставени така, че допирателната към линията на напрежение съвпада с посоката на вектора


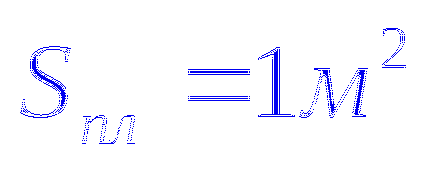

За точка такса силови линии са радиални линии. За положителни заряди - напускащи обвинението за безкрайността, за отрицателен - дойде при такса от безкрайността.
Н
По този начин броят на линии N изходящ от таксата винаги остава постоянна. т.е.
Това означава, че линиите на напрежение навсякъде с изключение на таксата не започва и свършва: положителен заряд, за да отидат до безкрайност, за центриране негативно от безкрайността и да прекратят срещу заплащане. В тази област линии не се пресичат помежду си. Това векторни линии имот е обща за всички електростатични полета, които полета, създадени от стационарна система за такси.
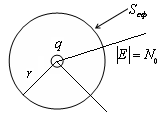
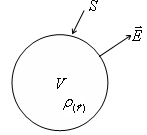
Да разгледаме повърхност, която е в S. електрическо поле

Общият брой на линии (1)
Експресия (1) се нарича вектор поток през повърхността S.
Поток вектор - скаларно количество.
Значението на поток вектор Е - броят на силови линии, които проникват тази повърхност S.
E
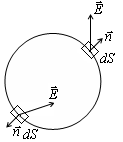

Експресионният вектор се нарича поток през затворена повърхност.
§2.2. Гаус теорема.
В предишния раздел, установихме, че за заплащане точка преминава през обхват (затворена повърхност) на:
Ако повърхността е с "мачка", линията на напрежение винаги се пресече границата повърхности нечетен брой пъти, а оттам и всяка повърхност, обграждаща заряд
Ако има система от такси, заобиколен произволна затворена повърхност S, на базата на принципа на суперпозиция може да се запише:
Експресия (2) се нарича Гаус "теорема: вектор поток през произволна повърхност е равна на сумата от алгебрични таксите в границите само на повърхността, разделен.
По-специално, ако няма такса вътре S, или;
Ако таксата е разпределена в рамките на повърхността е непрекъснато с обемната плътност. тогава общият заряд вътре и S. поток (* 2)
T
Гаус "теорема може да се изрази в диференциална форма. За това се използва теоремата Ostogradskogo-Gaussian, който свързва интеграл от затворена повърхност S с интеграла над V. обем Тази ограничена повърхност S.
Ако въведете символична nabla вектор оператор:
И най-накрая получаваме:
Връзка (3) е диференциалното формата на теоремата на Гаус.
Уравнения (2) и (* 2), (3) - един от основните съотношения електростатика. теорема на Гаус е валидна за следните причини:
Силата на взаимодействие между точката такси е обратно пропорционална на квадрата на разстоянието между такси.
Централният характер на силите на взаимодействие.
линейна суперпозиция на ефекти, дължащи се на различни такси.
Deep физическо значение на теоремата на Гаус. в природата, има електрически заряди и те са източник на електрическо поле.
Както ще бъде показано по-долу връзка (2) (* 2), (3) включени в така наречените Максуел уравнения класическата електродинамика като първото уравнение.
§ 2.3. Прилагане на правото на Гаус, за да намерите областта електростатично.
За електростатични заряди, които имат сферична и цилиндрична симетрия, Гаус теорема ни позволява да изчислим областта на обвинението в по-прост начин, отколкото ако са изчислени директно от закона на Кулон и принципа на суперпозиция.
а) Област на безкрайната верига е равномерно заредена.
Гъстотата на линеен заряд:
P
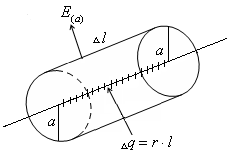

Ние се получи същия резултат въз основа на теоремата на Гаус. Очевидно е, че напрежението е перпендикулярна на спиралата. На разстояние един от спиралата. Следователно, проблемът е цилиндрична симетрия около ос, съвпадаща с резба.
Ние обграждат конец цилиндър с радиус а и дължина. Тъй като вектор, перпендикулярна на повърхността на цилиндър, силовите линии Eprohodyat само чрез страничната повърхност. Прилагането на Гаус теорема получаваме:
Имаме един и същ резултат.
б
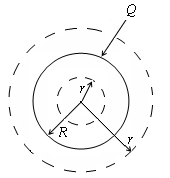
Сложете на метална топка заряд Q. Таксата се разпределя равномерно по повърхността на сфера. Във вътрешността на топката няма такса. След като е описано в центъра на областта около областта с произволен радиус R По този начин, областта в областта на метал дали е плътна или куха отсъства. По същия начин, прилагането на Гаус теоремата за точки извън сферата (R> R), ние откриваме: Полето извън сферата съвпада с областта на Р. точка заряд, разположен в центъра на сферата. Близо до повърхността (извън) е също така лесно да определи, ако Е R = R поставя в последния експресията. След това - повърхностната плътност такса върху сферата. и Този израз за E е валидна за всеки от заредената метална тялото. Трябва да се отбележи, че металното тяло на който и да е форма на различни точки на повърхността на тялото. в) Сега помислете безкрайна повърхнина, върху която такса е равномерно разпределена с плътност на повърхността. Намираме интензитет Е на произволно разстояние от самолет. Е лесно да се види, че векторът перпендикулярна на плоскостта.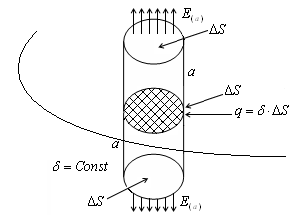
Ние избираме произволна област на самолет.
Построяване на базата на вертикален цилиндър и височина над повърхността и под него. В краищата на цилиндъра и се насочва от цилиндъра. Затова вектор поток минава само през краищата. Прилагаме Гаус теорема:
По този начин електрическото поле е независимо от разстоянието а на по всички точки на пространство над и под равнината на същото :. Такава област се нарича хомогенна.
ж) Да се определи електрическо поле Е вътре и е равномерно зарежда по обем радиус R. сфера на
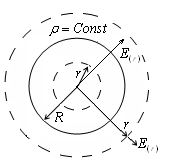
Ще опишем сфера около центъра на сферата с произволен радиус R Използване на Гаус теорема: Ако R По този начин, областта се зарежда от сфера обем съвпада с полето на точка заряд Q. намира в центъра на сферата. W г) областта между две успоредни равнини, зарежда с противоположни заряди. P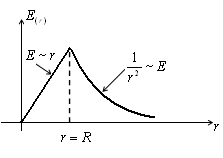
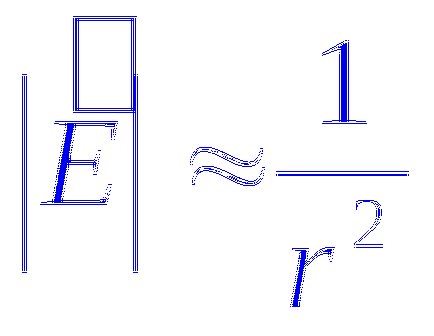
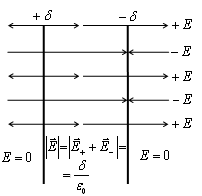

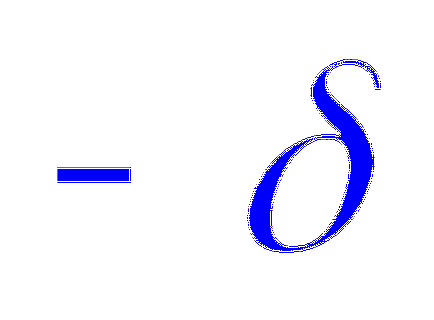

Забележка. Ако говорим за реално подреждане на две успоредни плочи, разстоянието между които е много по-малък от размера на плочи (равнинни кондензатор), областта електрически вътре в затворено плоча, и неговата интензивност
е) По подобен начин на електрическото поле изчислява mezhdukoaksialnymi (коаксиален) равномерно зарежда от дължината на линейна плътност radiusamii цилиндър.
Най-
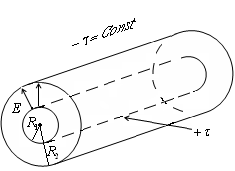
R е разстоянието от оста на цилиндъра.
Когато окончателното дължината на цилиндъра, такова устройство се нарича цилиндрична кондензатор.
ж) областта между две концентрични сфери с radiusamii.
E
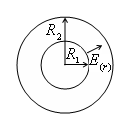


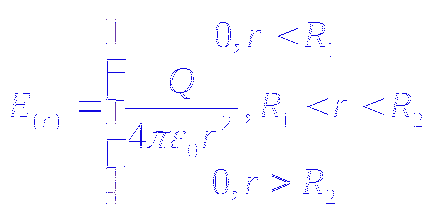
Такова устройство се нарича сферичен кондензатор.